Question

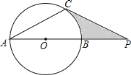
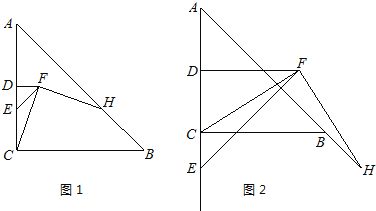
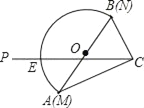
【题目】如图是一块含30°（即∠CAB=30°）角的三角板和一个量角器拼在一起，三角板斜边AB与量角器所在圆的直径MN重合，其量角器最外缘的读数是从N点开始（即N点的读数为0），现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止．在旋转过程中，射线CP与量角器的半圆弧交于E．

(1)当射线CP与△ABC的外接圆相切时，求射线CP旋转度数是多少？

(2)当射线CP分别经过△ABC的外心、内心时，点E处的读数分别是多少？

(3)当旋转7.5秒时，连接BE，求证：BE=CE．

Answer 1

【答案】(1)射线CP旋转度数是120°；(2)E处的读数为90；(3)证明见解析.

【解析】

(1) 连接OC. 根据切线的性质, 得∠OCP=, 根据等腰三角形的性质,得∠ACO=∠A, 从而求得射线CP旋转度数；

(2) 当CP过△ABC外心时 (即过O点)时,∠BCE=, 根据圆周角定理, 则点E处的读数是;当CP过△ABC的内心时, 即CP平分∠ACB, 则∠BCE=, 根据圆周角定理,则点E处的读数是.

(3) 根据已知, 知旋转了, 即可求得∠EBC=∠BCE=, 从而证明结论.

(1)连接OC．

∵射线CP与△ABC的外接圆相切，

∴∠OCP=90°，

∵OA=OC，

∴∠ACO=∠A=30°，

∴射线CP旋转度数是120°；

(2)

∵∠BCA=90°，

∴△ABC的外接圆就是量角器所在的圆．

当CP过△ABC外心时（即过O点），∠BCE=60°，

∴∠BOE=120°，即E处的读数为120，

当CP过△ABC的内心时，∠BCE=45°，∠EOB=90°，

∴E处的读数为90．

(3)在图2中，

∵∠PCA=2×7.5°=15°，∠BCE=75°，∠ECA=∠EBA=15°，

∴∠EBC=∠EBA+∠ABC=∠BCE=75°，

∴BE=EC．