题目内容
如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200米，从飞机上看地面控制点B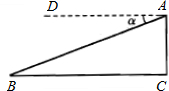
的俯角α=20°（B、C在同一水平线上），求目标C到控制点B的距离（精确到1米）．
（参考数据sin20°=0.34，cos20°=0.94，tan20°=0.36）
的俯角α=20°（B、C在同一水平线上），求目标C到控制点B的距离（精确到1米）．（参考数据sin20°=0.34，cos20°=0.94，tan20°=0.36）
∵AD∥BC，
∴∠B=∠α=20°．
在Rt△ACB中，
∠ACB=90°，tanB=
，
∴BC=
=
=
≈3333（米）．
答：目标C到控制点B的距离为3333米．
∴∠B=∠α=20°．
在Rt△ACB中，
∠ACB=90°，tanB=
| AC |
| BC |
∴BC=
| AC |
| tanB |
| 1200 |
| tan20° |
| 1200 |
| 0.36 |
答：目标C到控制点B的距离为3333米．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
要使教学楼不受货车的噪声影响，在此路段应该限速多少？（精确到10km/h）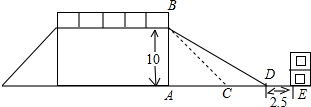
原坡脚10米的建筑物是否需要拆除？请说明理由．（参考数据：
方程x2-7x+12=0的两个根，且OA＞OB；
