题目内容
已知：在△ABC中，∠B为锐角，sinB=
，AB=15，AC=13，求BC的长．
| 4 |
| 5 |
过点A作AD⊥BC于D．
在△ADB中，∠ADB=90°，
∵sinB=
，AB=15，
∴AD=AB•sinB=15×
=12．
由勾股定理，可得BD=
=
=9．
在△ADC中，∠ADC=90°，AC=13，AD=12，
由勾股定理，可得DC=
=
=5．
∵AD＜AC＜AB，
∴当B、C两点在AD异侧时，可得BC=BD+CD=9+5=14．
当B、C两点在AD同侧时，可得BC=BD-CD=9-5=4．
∴BC边的长为14或4．
在△ADB中，∠ADB=90°，
∵sinB=
| 4 |
| 5 |
∴AD=AB•sinB=15×
| 4 |
| 5 |
由勾股定理，可得BD=
| AB2-AD2 |
| 152-122 |
在△ADC中，∠ADC=90°，AC=13，AD=12，
由勾股定理，可得DC=
| AC2-AD2 |
| 132-122 |
∵AD＜AC＜AB，
∴当B、C两点在AD异侧时，可得BC=BD+CD=9+5=14．
当B、C两点在AD同侧时，可得BC=BD-CD=9-5=4．
∴BC边的长为14或4．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
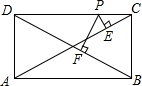
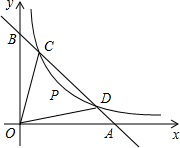，D（x2，y2），连接OC，OD（O是坐标原点），若∠BOC=∠AOD=α，且tanα=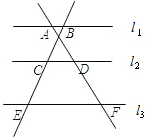
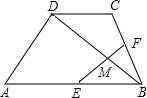
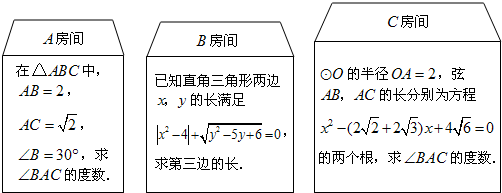
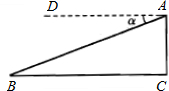的俯角α=20°（B、C在同一水平线上），求目标C到控制点B的距离（精确到1米）．