Question

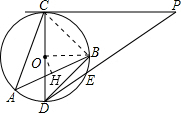
已知：如图，⊙O中，AB、AC是弦，CD是直径，PC是⊙O的切线，切点为C，割线PD交⊙O于点E，DE=

4

3

，PE=

14

3

，BD=2，∠ACD=15°．求AB的长（不取近似值）

Answer 1

连接BC，
∵CD是⊙O的直径，
∴∠CBD=90°，
又∵∠ABD=∠ACD=15°，
∴∠ABC=∠CBD-∠ABD=75°，
∵PC是⊙O的切线，
∴PC²=PE•PD，
∵PD=PE+DE=

14

3

+

4

3

=6，PE=

14

3

，
∴PC=

PE•PD

=2

7

，
又∵PC⊥CD，
∴∠PCD=90°，
在Rt△PCD中，由勾股定理，得CD=

PD2-PC2

=

62-(2 7 )2

=2

2

，
∴圆O的半径为

2

，
∵cos∠BDC=

BD

CD

=

2

2 2

=

2

2

，
∴∠BDC=45°，
∴∠BCD=90°-∠BDC=45°=∠BDC，
∴BC=BD=2，
连接BO，
∵CO=DO，
∴∠CBO=

1

2

∠CBD=45°，
∴∠ABO=∠ABC-∠CBO=30°，
作OH⊥AB，垂足为H，由垂径定理得到H为AB的中点，
∵cos∠ABO=

BH

BO

，
∴BH=BO•cos∠ABO=

2

•cos30°=

6

2

，
则AB=2BH=2×

6

2

=

6

．