题目内容
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E,设⊙O是△BDE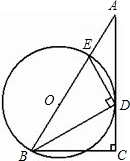 的外接圆.
的外接圆.
(1)求证:AC是⊙O的切线;
(2)若DE=2,BD=4,求AE的长.
 的外接圆.
的外接圆.(1)求证:AC是⊙O的切线;
(2)若DE=2,BD=4,求AE的长.
(1)证明:连接OD,
∵DE⊥DB,⊙O是△BDE的外接圆,
∴BE是直径,点O是BE的中点,
∵∠C=90°,
∴∠DBC+∠BDC=90°,
又BD为∠ABC的平分线,
∴∠ABD=∠DBC,
∵OB=OD,
∴∠ABD=∠ODB,
则∠ODB+∠BDC=90°即∠ODC=90°
又∵OD是⊙O的半径,
∴AC是⊙O的切线.(方法不唯一,参照给分)
(2)∵DE⊥DB,DE=2,BD=4,
∴BE=2
,OE=
,
∴∠ABD=∠ADE,又∠A为公共角,
∴△ADB∽△AED,则有
=
=
,
∴AD=2AE,
在Rt△AOD中,AO2=OD2+AD2,
即(
+AE)2=(
)2+(2AE)2,
解得AE=
或AE=0(舍去),
所以AE=
.

∵DE⊥DB,⊙O是△BDE的外接圆,
∴BE是直径,点O是BE的中点,
∵∠C=90°,
∴∠DBC+∠BDC=90°,
又BD为∠ABC的平分线,
∴∠ABD=∠DBC,
∵OB=OD,
∴∠ABD=∠ODB,
则∠ODB+∠BDC=90°即∠ODC=90°
又∵OD是⊙O的半径,
∴AC是⊙O的切线.(方法不唯一,参照给分)
(2)∵DE⊥DB,DE=2,BD=4,
∴BE=2
| 5 |
| 5 |
∴∠ABD=∠ADE,又∠A为公共角,
∴△ADB∽△AED,则有
| AE |
| AD |
| ED |
| DB |
| 2 |
| 4 |
∴AD=2AE,
在Rt△AOD中,AO2=OD2+AD2,
即(
| 5 |
| 5 |
解得AE=
| 2 |
| 3 |
| 5 |
所以AE=
| 2 |
| 3 |
| 5 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目