题目内容
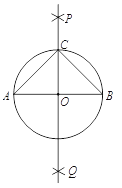
【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程．
已知：线段
．
求作：以为斜边的一个等腰直角三角形
．
作法：如图，
（1）分别以点
和点
为圆心，大于
的长为半径作弧，两弧相交于
，
两点；
（2）作直线
，交于点
；
（3）以为圆心，
的长为半径作圆，交直线于点
；
（4）连接
，
．
则
即为所求作的三角形．
请回答：在上面的作图过程中，①是直角三角形的依据是________；②是等腰三角形的依据是__________．
【答案】 直径所对的圆周角为直角 线段垂直平分线上的点与这条线段两个端点的距离相等
【解析】分析:首先作了线段AB的垂直平分线PQ,直角三角形外接圆的圆心就在斜边的中点处，接下来以
为圆心，
的长为半径作圆，交直线
于点
；
是直径所对的圆周角，则
同时点在线段
的垂直平分弦上，则
即为所求.
在上面的作图过程中，①是直角三角形的依据是直径所对的圆周角为直角,
②是等腰三角形的依据是线段垂直平分线上的点与这条线段两个端点的距离相等.
故答案为： (1). 直径所对的圆周角为直角； (2). 线段垂直平分线上的点与这条线段两个端点的距离相等.
阅读快车系列答案
【题目】已知
的三个顶点的坐标分别为
、
、
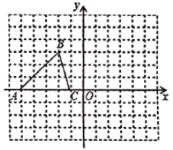
（1）画出关于坐标原点O成中心对称的
；
（2）将绕坐标原点O顺时针旋转
，画出对应的
；
（3）若以
、
、
、
为顶点的四边形为平行四边形，请直接写出在第一象限中的点的坐标 .
【题目】简单多面体是各个面都是多边形组成的几何体，十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）和棱数（E）之间存在一个有趣的关系式，称为欧拉公式．如表是根据左边的多面体模型列出的不完整的表：
多面体 | 顶点数 | 面数 | 棱数 |
四面体 | 4 | 4 | 6 |
长方体 | 8 | 6 | |
正八面体 | 8 | 12 |
现在有一个多面体，它的每一个面都是三角形，它的面数（F）和棱数（E）的和为30，则这个多面体的顶点数V＝_____．
【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
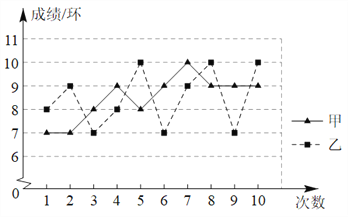
（1）根据折线图把下列表格补充完整；
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
（2）根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
