题目内容
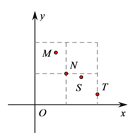
【题目】如图1，在平面直角坐标系中，直线y＝﹣
x+b与x轴、y轴相交于A、B两点，动点C（m，0）在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．
（1）求m和b的数量关系；
（2）当m＝1时，如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点B′的坐标及△BCD平移的距离；
（3）在（2）的条件下，直线AB上是否存在一点P，以P、C、D为顶点的三角形是等腰直角三角形？若存在，写出满足条件的P点坐标；若不存在，请说明理由．
【答案】（1）b=3m；（2）
个单位长度；（3）P(0,3)或（2，2）
【解析】
（1）易证△BOC≌△CED，可得BO=CE=b，DE=OC=m，可得点D坐标，代入解析式可求m和b的数量关系；
（2）首先求出点D的坐标，再求出直线B′C′的解析式，求出点C′的坐标即可解决问题；
（3）分两种情况讨论，由等腰直角三角形的性质可求点P坐标．
解：（1）直线y＝﹣
x+b中，x＝0时，y＝b，
所以，B（0，b），又C（m，0），
所以，OB＝b，OC＝m，
在
和
中
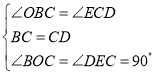
∴点
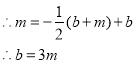
（2）∵m=1，
∴b=3，点C（1，0），点D（4，1）
∴直线AB解析式为：
设直线BC解析式为：y=ax+3，且过（1，0）
∴0=a+3
∴a=-3
∴直线BC的解析式为y=-3x+3，
设直线B′C′的解析式为y=-3x+c，把D（4，1）代入得到c=13，
∴直线B′C′的解析式为y=-3x+13，
当y=3时，
当y=0时，
∴△BCD平移的距离是
个单位．
（3）当∠PCD=90°，PC=CD时，点P与点B重合，
∴点P（0，3）
如图，当∠CPD=90°，PC=PD时，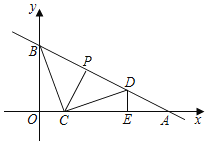
∵BC=CD，∠BCD=90°，∠CPD=90°
∴BP=PD
∴点P是BD的中点，且点B（0，3），点D（4，1）
∴点P（2，2）
综上所述，点P为（0，3）或（2，2）时，以P、C、D为顶点的三角形是等腰直角三角形．
