Question

【题目】如图，已知过点B（1，0）的直线与直线：相交于点P（－1，a）．且l1与y轴相交于C点，l2与x轴相交于A点．

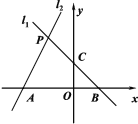
（1）求直线的解析式；

（2）求四边形的面积；

（3）若点Q是x轴上一动点，连接PQ、CQ，当△QPC周长最小时，求点Q坐标．

Answer 1

【答案】（1）y=-x+1；（2）；（3）点Q坐标为（－，0）时△QPC周长最小

【解析】

（1）根据点P在直线l2上，求出P的坐标，然后用待定系数法即可得出结论；

（2）根据计算即可；

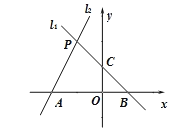
（3）作点C关于x轴对称点C＇，直线C’P与x轴的交点即为所求的点Q，求出点Q的坐标即可．

（1）∵点P（－1，a）在直线l2：y=2x+4上，∴，即，则P的坐标为（－1，2），设直线的解析式为：，那么，解得：，∴的解析式为：．

（2）∵直线与y轴相交于点C，∴C的坐标为（0，1）．

又∵直线与x轴相交于点A，∴A点的坐标为（－2，0），则AB=3，而，∴．

（3）作点C关于x轴对称点C′，易求直线C′P：y=-3x-1．当y=0时，x=，∴点Q坐标为（，0）时，△QPC周长最小．