题目内容
(9分)已知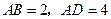 ,
,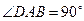 ,
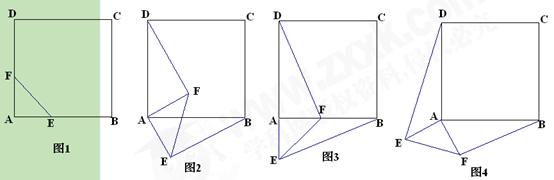
,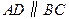 (如图).
(如图).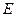 是射线
是射线 上的动点(点
上的动点(点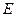 与点
与点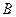 不重合),
不重合),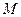 是线段
是线段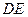 的中点.
的中点.
(1)设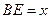 ,
,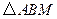 的面积为
的面积为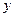 ,求
,求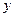 关于
关于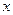 的函数关系式,并写出自变量
的函数关系式,并写出自变量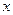 的取值范围;
的取值范围;
(2)如果以线段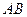 为直径的圆与以线段
为直径的圆与以线段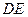 为
为 直径的圆外切,求线段
直径的圆外切,求线段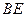 的长;
的长;
(3)连结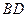 ,交线段
,交线段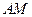 于点
于点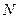 ,如果以
,如果以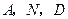 为顶点的三角形与
为顶点的三角形与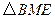 相似,求线段
相似,求线段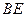 的长.
的长.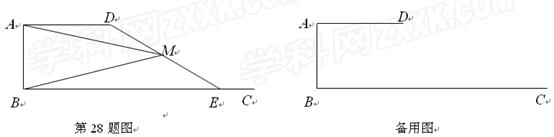
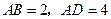 ,
,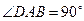 ,
,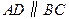 (如图).
(如图).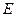 是射线
是射线 上的动点(点
上的动点(点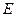 与点
与点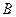 不重合),
不重合),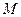 是线段
是线段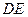 的中点.
的中点.(1)设
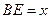 ,
,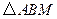 的面积为
的面积为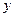 ,求
,求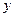 关于
关于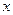 的函数关系式,并写出自变量
的函数关系式,并写出自变量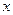 的取值范围;
的取值范围;(2)如果以线段
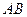 为直径的圆与以线段
为直径的圆与以线段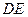 为
为 直径的圆外切,求线段
直径的圆外切,求线段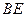 的长;
的长;(3)连结
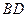 ,交线段
,交线段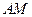 于点
于点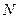 ,如果以
,如果以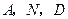 为顶点的三角形与
为顶点的三角形与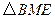 相似,求线段
相似,求线段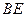 的长.
的长.
解:(1)取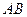 中点
中点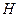 ,连结
,连结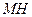 ,
,
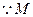 为
为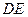 的中点,
的中点, ,
,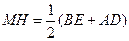 .································ 1分
.································ 1分
又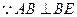 ,
, .·································································· 2分
.·································································· 2分
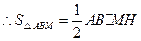 ,得
,得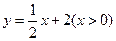 ;··············································· 3分
;··············································· 3分
(2)过D作DP ⊥BC,垂足为P,
⊥BC,垂足为P, ∠DAB=∠ABC=∠BPD=90°,
∠DAB=∠ABC=∠BPD=90°,
∴四边形ABPD是矩形.
 以线段
以线段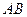 为直径的圆与以线段
为直径的圆与以线段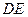 为直径的圆外切,
为直径的圆外切,
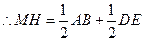 ,又
,又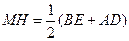 ,∴DE=BE+AD-AB=x+4-2=x+2……4分
,∴DE=BE+AD-AB=x+4-2=x+2……4分
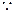 PD=AB=2,PE= x-4,DE2= PD2+ PE2,…………………………………………………5分
PD=AB=2,PE= x-4,DE2= PD2+ PE2,…………………………………………………5分
∴(x+2)2=22+(x-4)2,解得: .
.
∴线段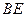 的长为
的长为 .…………………………………………………………………………6分
.…………………………………………………………………………6分
(3)由已知,以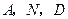 为顶点的三角形与
为顶点的三角形与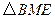 相似,
相似,
又易证得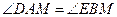 .···································································
.···································································  7分
7分
由此可知,另一对对应角相等有两种情况:①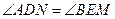 ;②
;②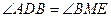 .
.
①当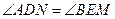 时,
时, ,
,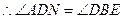 .
.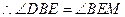 .
.
 ,易得
,易得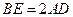 .得
.得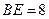 ;················································ 8分
;················································ 8分
②当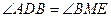 时,
时, ,
,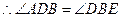 .
.
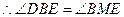 .又
.又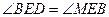 ,
,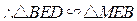 .
.
 ,即
,即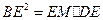 =
= ,得x2=
,得x2= [22+(x-4)2].
[22+(x-4)2].
解得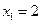 ,
, (舍去).即线段
(舍去).即线段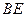 的长为2.······································· 9分
的长为2.······································· 9分
综上所述,所求线段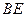 的长为8或2.
的长为8或2.
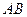 中点
中点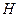 ,连结
,连结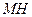 ,
,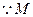 为
为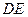 的中点,
的中点, ,
,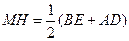 .································ 1分
.································ 1分又
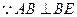 ,
, .·································································· 2分
.·································································· 2分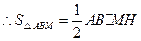 ,得
,得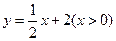 ;··············································· 3分
;··············································· 3分(2)过D作DP
 ⊥BC,垂足为P,
⊥BC,垂足为P, ∠DAB=∠ABC=∠BPD=90°,
∠DAB=∠ABC=∠BPD=90°,∴四边形ABPD是矩形.
 以线段
以线段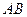 为直径的圆与以线段
为直径的圆与以线段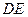 为直径的圆外切,
为直径的圆外切,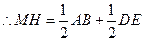 ,又
,又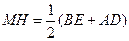 ,∴DE=BE+AD-AB=x+4-2=x+2……4分
,∴DE=BE+AD-AB=x+4-2=x+2……4分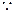 PD=AB=2,PE= x-4,DE2= PD2+ PE2,…………………………………………………5分
PD=AB=2,PE= x-4,DE2= PD2+ PE2,…………………………………………………5分∴(x+2)2=22+(x-4)2,解得:
 .
.∴线段
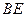 的长为
的长为 .…………………………………………………………………………6分
.…………………………………………………………………………6分(3)由已知,以
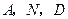 为顶点的三角形与
为顶点的三角形与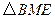 相似,
相似,又易证得
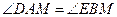 .···································································
.···································································  7分
7分由此可知,另一对对应角相等有两种情况:①
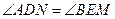 ;②
;②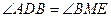 .
.①当
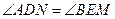 时,
时, ,
,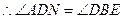 .
.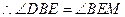 .
. ,易得
,易得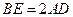 .得
.得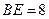 ;················································ 8分
;················································ 8分②当
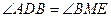 时,
时, ,
,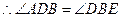 .
.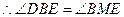 .又
.又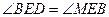 ,
,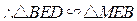 .
. ,即
,即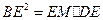 =
= ,得x2=
,得x2= [22+(x-4)2].
[22+(x-4)2].解得
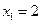 ,
, (舍去).即线段
(舍去).即线段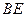 的长为2.······································· 9分
的长为2.······································· 9分综上所述,所求线段
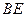 的长为8或2.
的长为8或2.略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 的顶点
的顶点 在原点,点
在原点,点 的坐标为
的坐标为 ,点
,点 的纵坐标是
的纵坐标是 ,则顶点
,则顶点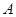 的坐标是
的坐标是 


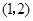

 的模相等的向量是▼.
的模相等的向量是▼. ?说明理由;
?说明理由;


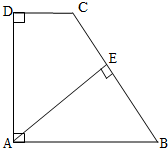
 B和AD上,且AE=AF.此时,线段BE、DF的数量关
B和AD上,且AE=AF.此时,线段BE、DF的数量关 系和位置关系分别是什么?请直接写出结论.
系和位置关系分别是什么?请直接写出结论.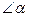 ,当
,当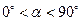 时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由. 角形FAE绕直角顶点A顺时针旋转
角形FAE绕直角顶点A顺时针旋转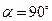 时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
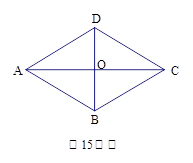
时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.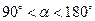 时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.