题目内容
(11·丹东)(本题12分)已知:正方形ABCD.
(1)如图1,点E、点F分别在边A B和AD上,且AE=AF.此时,线段BE、DF的数量关
B和AD上,且AE=AF.此时,线段BE、DF的数量关 系和位置关系分别是什么?请直接写出结论.
系和位置关系分别是什么?请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转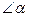 ,当
,当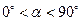 时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三 角形FAE绕直角顶点A顺时针旋转
角形FAE绕直角顶点A顺时针旋转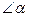 ,当
,当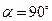 时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转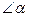 ,当
,当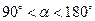 时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.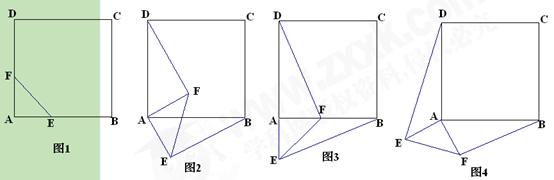
(1)如图1,点E、点F分别在边A
 B和AD上,且AE=AF.此时,线段BE、DF的数量关
B和AD上,且AE=AF.此时,线段BE、DF的数量关 系和位置关系分别是什么?请直接写出结论.
系和位置关系分别是什么?请直接写出结论.(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转
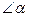 ,当
,当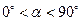 时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.(3)如图3,等腰直角三
 角形FAE绕直角顶点A顺时针旋转
角形FAE绕直角顶点A顺时针旋转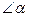 ,当
,当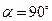 时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转
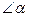 ,当
,当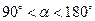 时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
(1)BE=DF且BE⊥DF
(2)成立
证明:延长DF交AB于点H,交BE于点G.

在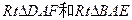 中,
中,
∵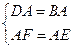
∴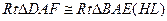
∴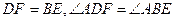
又∵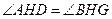
∴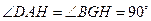
∴BE=DF且BE⊥DF仍成立
(3)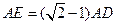
(4)菱形
(2)成立
证明:延长DF交AB于点H,交BE于点G.

在
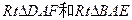 中,
中, ∵
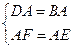
∴
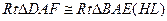
∴
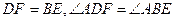
又∵
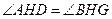
∴
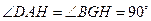
∴BE=DF且BE⊥DF仍成立
(3)
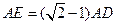
(4)菱形
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
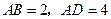 ,
,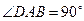 ,
,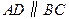 (如图).
(如图).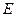 是射线
是射线 上的动点(点
上的动点(点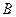 不重合),
不重合),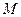 是线段
是线段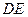 的中点.
的中点.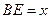 ,
,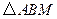 的面积为
的面积为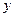 ,求
,求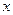 的函数关系式,并写出自变量
的函数关系式,并写出自变量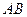 为直径的圆与以线段
为直径的圆与以线段 直径的圆外切,求线段
直径的圆外切,求线段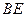 的长;
的长;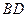 ,交线段
,交线段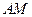 于点
于点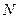 ,如果以
,如果以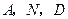 为顶点的三角形与
为顶点的三角形与 相似,求线段
相似,求线段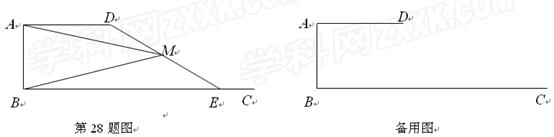

 DF交BC于点F.
DF交BC于点F.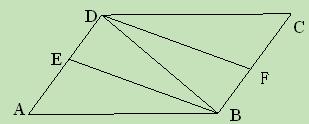

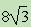 ,求AC的长.
,求AC的长.

 .
.
 ?若存在,请求出该点坐标,若不存在,请说明理由.
?若存在,请求出该点坐标,若不存在,请说明理由.