题目内容
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.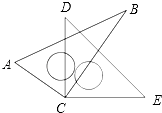
(1)写出以C为顶点的相等的锐角,并说明理由;
(2)若射线CB平分∠DCE,求∠ACE的度数.
【答案】
(1)解:∠ACD=∠BCE,
∵∠ACB=∠DCE=90°,
∴∠ACD+∠DCE=90°,
∠BCE+∠DCE=90°,
∴∠ACD=∠BCE
(2)解:∵CB平分∠DCE,
∴∠BCE= ![]() ∠DCE=45°,
∠DCE=45°,
∴∠ACE=∠ACB+∠BCE=135°
【解析】(1)根据同角的余角相,即可得出答案。
(2)根据角平分线的定义求出∠BCE的度数,再根据∠ACE=∠ACB+∠BCE,计算即可得出∠ACE的度数。
【考点精析】根据题目的已知条件,利用角的平分线和角的运算的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

练习册系列答案
相关题目