题目内容
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. 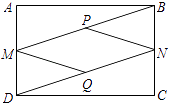
(1)求证:△MBA≌△NDC;
(2)求证:四边形MPNQ是菱形.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM= ![]() AD,CN=
AD,CN= ![]() BC,
BC,
∴AM=CN,
在△MAB和△NDC中,
∵ 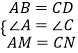 ,
,
∴△MBA≌△NDC(SAS)
(2)证明:四边形MPNQ是菱形.
理由如下:连接AP,MN,
则四边形ABNM是矩形,
∵AN和BM互相平分,
则A,P,N在同一条直线上,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵ 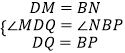 ,
,
∴△MQD≌△NPB(SAS).
∴四边形MPNQ是平行四边形,
∵M是AD中点,Q是DN中点,
∴MQ= ![]() AN,
AN,
∴MQ= ![]() BM,
BM,
∵MP= ![]() BM,
BM,
∴MP=MQ,
∴平行四边形MQNP是菱形.
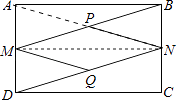
【解析】(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;(2)四边形MPNQ是菱形,连接AN,有(1)可得到BM=DN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目