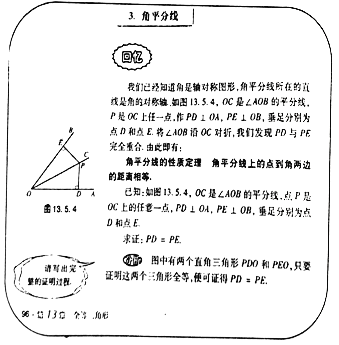
题目内容
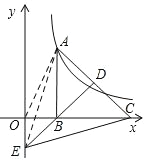
【题目】如图,抛物线L:y=﹣(x﹣2)2+m2+2m与x轴交于A,B,直线y=kx﹣1与y轴交于E,与L的对称轴交于点F(n,3),与L交于D,抛物线L的对称轴与L交于P.
(1)求k的值.
(2)点P能否与点F关于x轴的对称点重合?若认为能,请求出m的值;若认为不能,说明理由.
(3)小林研究了抛物线L的解析式后,得到了如下的结论:因为m可以取任意实数,所以点C可以在y轴上任意移动,即C点可以到达y轴的任何位置,你认为他说的有道理吗?说说你的想法.
(4)当抛物线L与直线y=kx﹣1有两个公共点时,直接写出适合条件的m的最大整数.
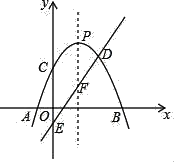
【答案】(1)k=2;(2)不能,理由见解析;(3)没道理,见解析;(4)适合条件的m的最大整数值是1.
【解析】
(1)首先得出对称轴方程,从而求得F点坐标,代入一次函数解析式,求k值;
(2)由对称点坐标关系可得点F关于x轴的对称点坐标,再与点P坐标比较,即可进行 判断;
(3)把L的解析式化成顶点式,就可以知道函数的最小值是-5,所以点C都不能到达(0,﹣5)以下的位置;
(4)两图像有公共点,即函数值相等,得到一元二次方程,
解:(1)抛物线L的对称轴是x=2,所以n=2,点F(2,3),代入y=kx﹣1中,得3=2k﹣1,
解得k=2;
(2)不能,理由:点P的坐标为(2,m2+2m),点F关于x轴的对称点F'的坐标是(2,﹣3),
若点P与点F'重合,则m2+2m=﹣3,
即:(m+1)2=﹣2.显然不可能;
(3)没道理,
因为,点C的纵坐标为yC=m2+2m﹣4=(m+1)2﹣5
因为yC的最小值为﹣5,所以无论m取何值,点C都不能到达(0,﹣5)以下的位置.
(4)直线y=kx﹣1的解析式为y=2x﹣1
当﹣(x﹣2)2+m2+2m=2x﹣1时,得x2﹣2x﹣(m2+2m﹣3)=0,
△=22﹣4×1×(m2+2m﹣3)=﹣4[(m+1)2﹣5]
当△≥0时,(m+1)2﹣5≤0,所以适合条件的m的最大整数值是1.