��Ŀ����
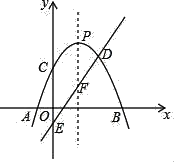
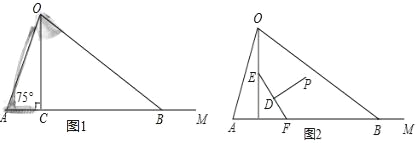
����Ŀ����ͼ1Ϊ������ˮƽ�����ϵ�̨�Ƶ�ƽ��ʾ��ͼ���Ʊ�AO��Ϊ50cm����ˮƽ�������γɵļн���OAM Ϊ75�㣮�ɹ�ԴO����ı�Ե����OC��OB ��ˮƽ�������γɵļн���OCA����OBA�ֱ�Ϊ90���30�㣮���������������أ������ȷ��0.1cm��sin75����0.97��cos75���0.26��![]() ��1.73��
��1.73��
��1�����̨������ˮƽ����Ŀ���BC��
��2�������ڴ�̨���¿��飬�������������ͼ2��ʾ�ļ���ͼ�Σ�����EF��ˮƽ����ļн���EFCΪ60�㣬��ij���EFΪ24cm����PΪ�۾�����λ�ã���P��EF�Ĵ�ֱƽ�����ϣ��ҵ�EF����ԼΪ34cm�����۾���ˮƽ����ľ��룮
���𰸡���1����̨������ˮƽ��Ŀ���BC��Լ��83.9cm����2���۾���ˮƽ����ľ����Լ��27.38cm��
��������
��1����ֱ��������ACO�У�����sin75��=![]() �����OC����ֱ��������BCO�У�tan30��=
�����OC����ֱ��������BCO�У�tan30��=![]() �����BC���ɣ�
�����BC���ɣ�
��2����ͼ������P��PH��AB��H����OB��M������D��DG��PH��G��DQ��AB��Q�����ı���DGHQΪ���Σ���GDF=��EFC=��DPG=60�㣬���PH�ij�������⣮
��1����ֱ��������ACO�У�sin75��= ![]() ��
��
���OC=50��0.97��48.5��
��ֱ��������BCO�У�tan30��=![]() ��
��
���BC=1.73��48.5��83.9��
�𣺸�̨������ˮƽ��Ŀ���BC��Լ��83.9cm��
��2����ͼ2������P��PH��AB��H������D��DG��PH��G��DQ��AB��Q��
���ı���DGHQΪ���Σ���GDF=��EFC=��DPG=60��
������DE=DF=12cm��DP=34cm��
��PG=17cm��QH=DG=17![]() cm��QF=6cm��GH=DQ=6
cm��QF=6cm��GH=DQ=6![]() cm��
cm��
��PH=PH+GH=17+6![]() ��27.38cm��
��27.38cm��
���۾���ˮƽ����ľ����Լ��27.38cm��