Question

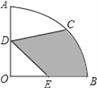
【题目】如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为_____cm2．

Answer 1

【答案】π+﹣

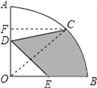
【解析】连结OC，过C点作CF⊥OA于F，

∵半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，

∴OD=OE=1cm，OC=2cm，∠AOC=45°，

∴CF=，

∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积

=﹣

=π﹣（cm2）

三角形ODE的面积=OD×OE=（cm2），

∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积

=﹣（π﹣）﹣

=π+﹣（cm2）．

故图中阴影部分的面积为（π+﹣）cm2．

故答案为：（π+﹣）．