题目内容
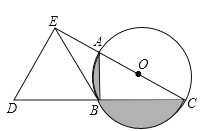
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接BO,根据△OBC和△BCE都是等腰三角形,即可得到∠BEC=∠OBC=∠OCB=30°,再根据三角形内角和即可得到∠EBO=90°,进而得出BE是⊙O的切线;
(2)在Rt△ABC中,根据∠ACB=30°,BC=3,即可得到半圆的面积以及Rt△ABC的面积,进而得到阴影部分的面积.
试题解析:(1)如图所示,连接BO,
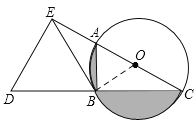
∵∠ACB=30°,
∴∠OBC=∠OCB=30°,
∵DE⊥AC,CB=BD,
∴Rt△DCE中,BE=![]() CD=BC,
CD=BC,
∴∠BEC=∠BCE=30°,
∴△BCE中,∠EBC=180°﹣∠BEC﹣∠BCE=120°,
∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°,
∴BE是⊙O的切线;
(2)当BE=3时,BC=3,
∵AC为⊙O的直径,
∴∠ABC=90°,
又∵∠ACB=30°,
∴AB=tan30°×BC=![]() ,
,
∴AC=2AB=2![]() ,AO=
,AO=![]() ,
,
∴阴影部分的面积=半圆的面积﹣Rt△ABC的面积=![]() π×AO2﹣
π×AO2﹣![]() AB×BC=
AB×BC=![]() π×3﹣
π×3﹣![]() ×
×![]() ×3=
×3=![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目