Question

【题目】如图，反比例函数y= （k≠0，x＞0）的图像与直线y=3x相交于点C，过直线上点A（1，3）作AB⊥x轴于点B，交反比例函数图像于点D，且AB=3BD．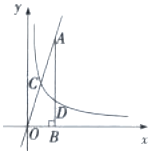
（1）求k的值；
（2）求点C的坐标；
（3）在y轴上确定一点M，使点M到C、D两点距离之和d=MC+MD最小，求点M的坐标．

Answer 1

【答案】
（1）解：∵A（1，3），

∴AB=3，OB=1，

∵AB=3BD，

∴BD=1，

∴D（1，1）

将D坐标代入反比例解析式得：k=1

（2）解：由（1）知，k=1，

∴反比例函数的解析式为；y= ，

解： ，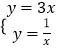

解得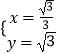： 或 ，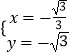

∵x＞0，

∴C（ ， ）

（3）解：如图，作C关于y轴的对称点C′，连接C′D交y轴于M，

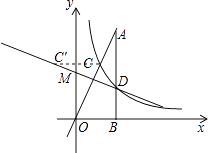
则d=MC+MD最小，

∴C′（﹣ ， ），

设直线C′D的解析式为：y=kx+b，

∴ ，∴ ，

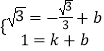∴y=（3﹣2 ）x+2 ﹣2，

当x=0时，y=2 ﹣2，

∴M（0，2 ﹣2）．

【解析】（1）根据A坐标，以及AB=3BD求出D坐标，代入反比例解析式求出k的值；（2）直线y=3x与反比例解析式联立方程组即可求出点C坐标；（3）作C关于y轴的对称点C′，连接C′D交y轴于M，则d=MC+MD最小，得到C′（﹣ ， ），求得直线C′D的解析式为y=﹣ x+1+ ，直线与y轴的交点即为所求．
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识，掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．