题目内容
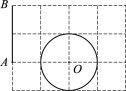
【题目】如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为_____.
【答案】60°或120 °
【解析】
线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,切点为C′和C″,连接OC′、OC″,根据切线的性质得OC′⊥AB′,OC″⊥AB″,利用直角三角形30度的判定或三角函数求出∠OAC′=30°,从而得到∠BAB′=60°,同理可得∠OAC″=30°,则∠BAB″=120°.
线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,切点为C′和C″,连接OC′、OC″,
则OC′⊥AB′,OC″⊥AB″,
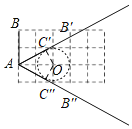
在Rt△OAC′中,∵OC′=1,OA=2,
∴∠OAC′=30°,
∴∠BAB′=60°,
同理可得∠OAC″=30°,
∴∠BAB″=120°,
综上所述,α的值为60°或120°.
故答案为60°或120°.

练习册系列答案
相关题目