题目内容
【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
【答案】(﹣2,1)或(14,﹣7).
【解析】
先计算△ABC的面积,根据x的正、负分两种情况进行讨论:
第一种情况:当x<0时,如图2,根据S△ABP=S梯形AEFB-S△AEP-S△BFP,列方程可得结论;
第二种情况:当x>0时,如图3,同理可得结论.
也可以作AB的平行线(两条),根据AB的解析式:y=-x+3,根据面积可求得平行线与y轴的交点,可得平行线的解析式为:y=-x-1和y=-x+7,最后利用P点的坐标解决问题.
解:如图1,
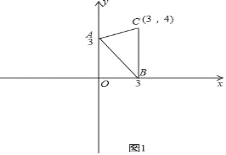
∵A(0,3),B(3,0),C(3,4),
∴BC=4,A到BC的距离为3,
∴△ABC的面积为 ![]() =6,
=6,
分为两种情况:第一种情况:当x<0时,如图2,
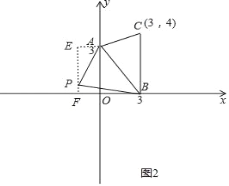
过P作PF⊥x轴于F,过A作AE⊥PF于E,
∵A(0,3),B(3,0),P(x,﹣0.5x),
∴AE=﹣x,EF=3,BF=3﹣x,PF=﹣0.5x,PE=3﹣(﹣0.5x)=3+0.5x,
∴S△ABP=S梯形AEFB﹣S△AEP﹣S△BFP
=![]() (﹣x+3﹣x)3﹣
(﹣x+3﹣x)3﹣![]() (﹣x)(3+0.5x)﹣
(﹣x)(3+0.5x)﹣![]() (3﹣x)(﹣0.5x)
(3﹣x)(﹣0.5x)
=﹣![]() x+
x+![]() ,
,
∵△ABP的面积等于△ABC的面积,△ABC的面积为6,
∴﹣![]() x+
x+![]() =6,
=6,
解得:x=﹣2,
﹣0.5x=1,
所以此时P点的坐标为(﹣2,1);
第二种情况:当x>0时,如图3,

作矩形AEPF(E在y轴上),
S△ABP=S矩形AEPF﹣S△AFP﹣S梯形OEPB﹣S△AOB=(3+0.5x)x﹣![]() x(3+0.5x)﹣
x(3+0.5x)﹣![]() (3+x)0.5x﹣
(3+x)0.5x﹣![]() =6,
=6,
解得:x=14,
所以此时P点的坐标为(14,﹣7);
综上所述,则P点的坐标是(﹣2,1)或(14,﹣7).
故答案为:(﹣2,1)或(14,﹣7).

 53随堂测系列答案
53随堂测系列答案【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).