��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���P��ͼ��W���м��Ķ������£�Q��ͼ��W��һ�㣬��MΪ�߶�PQ���е㣬���MΪ��P��ͼ��W���м�㣮C��-2��3����D��1��3����E��1��0����F��-2��0��
��1����A��2,0����
�ٵ�A��ԭ����м�������Ϊ ��
�����A���߶�CD���м��ĺ�����m��ȡֵ��Χ��
��2����BΪֱ��y=2x��һ�㣬���ı���CDEF�ı��ϴ��ڵ�B���ı���CDEF���м�㣬ֱ��д����B�ĺ�����n��ȡֵ��Χ��

���𰸡���1���٣�1��0������![]() ����2��
����2��![]() ��1��n��3.
��1��n��3.
��������
��1���ٸ��ݵ�A��O�����꣬�����е����깫ʽ����������ۣ�
���������⻭��ͼ�Σ��۲�ͼ�ο�֪��A���߶�CD���м������ɵ�ͼ�����߶�C��D�������ݵ�A��C��D�����꣬�����е����깫ʽ�������C����D�������꣬�����ɵó�m��ȡֵ��Χ��
��2������һ�κ���ͼ���ϵ�����������ɵó���B������Ϊ��n��2n�����������⻭��ͼ�Σ��۲�ͼ�ο�֪����B���ı���CDEF���м��ֻ���ڱ�EF��DE�ϣ�����B���ı���CDEF���м���ڱ�EF��ʱ�������ı���CDEF��������ķ�Χ���ɵó�����n��һԪһ�β���ʽ�飬��֮���ɵó�n��ȡֵ��Χ������B���ı���CDEF���м���ڱ�DE��ʱ�����ı���CDEF�ĺᡢ������ķ�Χ���ɵó�����n��һԪһ�β���ʽ�飬��֮���ɵó�n��ȡֵ��Χ�����ϣ�����ý⣮
��1���١ߵ�A������Ϊ��2��0����
���A��ԭ����м�������Ϊ��![]() ��
��![]() ��������1��0����
��������1��0����
�ʴ�Ϊ����1��0����
����ͼ1����A���߶�CD���м������ɵ�ͼ�����߶�C��D����
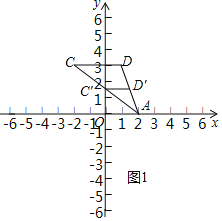
�������֪����C��Ϊ�߶�AC���е㣬��D��Ϊ�߶�AD���е㣮
�ߵ�A������Ϊ��2��0������C������Ϊ��-2��3������D������Ϊ��1��3����
���C����������0��![]() ������D����������
������D����������![]() ��
��![]() ����
����
���A���߶�CD���м��ĺ�����m��ȡֵ��ΧΪ0��m��![]() ��
��
��2���ߵ�B�ĺ�����Ϊn��
���B��������n��2n����
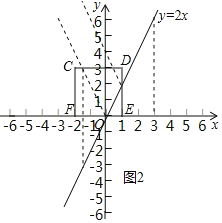
����B���ı���CDEF���м���ڱ�EF��ʱ����![]() ��
��
��ã�-![]() ��n��0��
��n��0��
����B���ı���CDEF���м���ڱ�DE��ʱ����![]() ��
��
��ã�1��n��3��
������������B�ĺ�����n��ȡֵ��ΧΪ-![]() ��n��0��1��n��3��
��n��0��1��n��3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�