��Ŀ����
����Ŀ����ѧ����ѧϰ��Բ�ܽǵĸ�������ʣ���������Բ�ϣ�������Բ�ཻ������ͬ�����Ե�Բ�ܽ��������С���ڿκ������Բ��Ǻ�Բ�ڽǽ�����̽����
����������̽�����̣��벹��������
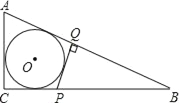
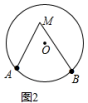
������������Բ�⣬������Բ�ཻ�Ľǽ���Բ��ǣ�������Բ�ڣ�������Բ�ཻ�Ľǽ���Բ�ڽǣ���ͼ1����MΪ![]() ���Ե�һ��Բ��ǣ�
���Ե�һ��Բ��ǣ�
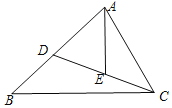
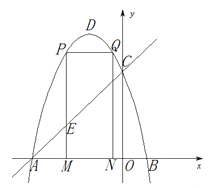
(1)����ͼ2�л���![]() ���Ե�һ��Բ�ڽǣ�
���Ե�һ��Բ�ڽǣ�
�������
(2)ͨ����λ�ͼ��������������������룺һ�������Ե�Բ���______���������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽ�______���������Ե�Բ�ܽǣ�(������������������������С����)
����֤����
(3)����ͼ1��ͼ2��������������������ѡһ������֤����
������
����֤���������������붼����ȷ�ģ�����̽�����֣������Խ����������⣮
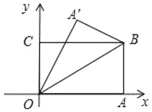
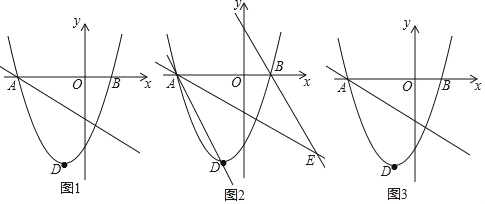
(4)��ͼ3��F��H�ǡ�CDE�ı�DC�����㣬�ڱ�DE����һ��Pʹ�á�FPH�����������ȷ����P��λ�ã�(д��˼·���ɣ���Ҫ��д�������ͻ�ͼ)

���𰸡���1����������2��С�ڣ����ڣ�3����������4��������
��������
��1���ڡ�O����ȡһ��M������AM��BM��
��2���۲�ͼ�Σ���֪��һ�������Ե�Բ���С�����������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽǴ������������Ե�Բ�ܽǣ����ʵý⣻
��3����i��BM���O�ཻ�ڵ�C������AC��������������ǵ����ʿɵó���ACB=��M+��MAC��������֤����ACB����M����ii���ӳ�BM����O�ڵ�C������AC��������������ǵ����ʿɵó���AMB=��ACB+��CAM��������֤����AMB����ACB��
��4���ɣ�2���Ľ��ۣ���֪��������F��H��Բ��DE����ʱ���е㼴Ϊ����ĵ�P��
��1����ͼ2��ʾ��
��2���۲�ͼ�Σ���֪��һ�������Ե�Բ���С�����������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽǴ������������Ե�Բ�ܽǣ�
�ʴ�Ϊ��С�ڣ����ڣ�
��3��֤������i����ͼ1��BM���O�ཻ�ڵ�C������AC��
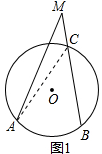
�ߡ�ACB����M+��MAC��
���ACB����M��
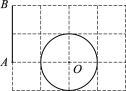
��ii����ͼ4���ӳ�BM����O�ڵ�C������AC��
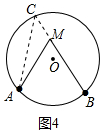
�ߡ�AMB����ACB+��CAM��
���AMB����ACB��
��4����ͼ3��������F��H��Բ��DE����ʱ���е㼴Ϊ����ĵ�P��

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�