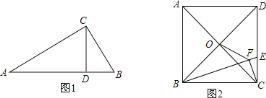题目内容
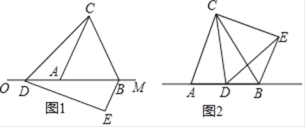
【题目】已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．
（1）如图1，求证：△CDE是等边三角形．
（2）设OD＝t，
①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．
②求t为何值时，△DEB是直角三角形（直接写出结果即可）．
【答案】(1)见解析;(2) ①见解析; ②t＝2或14.
【解析】
（1）由旋转的性质得到∠DCE=60°，DC=EC，即可得到结论；
（2）①当6＜t＜10时，由旋转的性质得到BE=AD，于是得到C△DBE=BE+DB+DE=AB+DE=4+DE，根据等边三角形的性质得到DE=CD，由垂线段最短得到当CD⊥AB时，△BDE的周长最小，于是得到结论；
②存在，当点D与点B重合时，D，B，E不能构成三角形；当0≤t＜6时，由旋转的性质得到∠ABE=60°，∠BDE＜60°，求得∠BED=90°，根据等边三角形的性质得到∠DEB=60°，求得∠CEB=30°，求得OD=OA-DA=6-4=2=t；当6＜t＜10时，此时不存在；当t＞10时，由旋转的性质得到∠DBE=60°，求得∠BDE＞60°，于是得到t=14．
（1）∵将△ACD绕点C逆时针方向旋转60°得到△BCE，
∴∠DCE＝60°，DC＝EC，
∴△CDE是等边三角形；
（2）①存在，当6＜t＜10时，
由旋转的性质得，BE＝AD，
∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，
由（1）知，△CDE是等边三角形，
∴DE＝CD，
∴C△DBE＝CD+4，
由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，
此时，CD＝2
，
∴△BDE的最小周长＝CD+4＝2+4；
②存在，∵当点D与点B重合时，D，B，E不能构成三角形，
∴当点D与点B重合时，不符合题意；
当0≤t＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，
∴∠BED＝90°，
由（1）可知，△CDE是等边三角形，
∴∠DEB＝60°，
∴∠CEB＝30°，
∵∠CEB＝∠CDA，
∴∠CDA＝30°，
∵∠CAB＝60°，
∴∠ACD＝∠ADC＝30°，
∴DA＝CA＝4，
∴OD＝OA﹣DA＝6﹣4＝2，
∴t＝2；
当6＜t＜10时，由∠DBE＝120°＞90°，
∴此时不存在；
当t＞10时，由旋转的性质可知，∠DBE＝60°，
又由（1）知∠CDE＝60°，
∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，
而∠BDC＞0°，
∴∠BDE＞60°，
∴只能∠BDE＝90°，
从而∠BCD＝30°，
∴BD＝BC＝4，
∴OD＝14，
∴t＝14，
综上所述：当t＝2或14时，以D、E、B为顶点的三角形是直角三角形．
