题目内容
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上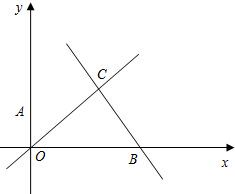 移动(0<x<3),过点P作直线l与x轴垂直.
移动(0<x<3),过点P作直线l与x轴垂直.(1)求点C的坐标;
(2)若A点坐标为(0,1),当点P运动到什么位置时,AP+CP最小;
(3)设△OBC中位于直线l左侧部分的面积为S,求S与x之间的函数关系式.
分析:(1)将两直线的y相等即可求出C的坐标;
(2)画出A关于x轴的对称点,然后连接C,与x轴交点就是要求的点P;
(3)分情况讨论,当l在C左侧和l在C右侧两种情况.
(2)画出A关于x轴的对称点,然后连接C,与x轴交点就是要求的点P;
(3)分情况讨论,当l在C左侧和l在C右侧两种情况.
解答:解:(1)两直线的解析式相等可得:x=-2x+6,
解得x=2,所以y=2,
所以C的坐标是(2,2)
(2)点A关于x轴的对称点A1为(0,-1),
直线A1C的解析式为y=
x-1,
直线A1C与x轴的交点坐标是(
,0),
所以当点P运动到(
,0)时,AP+CP最小;
(3)∵C(2,2),B(3,0),
∴OB=3,
∴S△OCB=
×3×2=3,
当0<x≤2时,即l在点C左侧,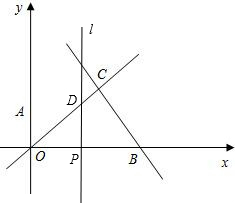
∵点P坐标为(x,0),
∴与直线y=x的交点D的坐标是(x,x),
∴S=
•x•x=
x2;
当2<x<3时,即l在点C右侧,
∵P(x,0),
∴直线l与直线BC的交点D的坐标是(x,-2x+6),
∴S△BDP=
×PB×PD=
•(3-x)•(-2x+6)=(3-x)2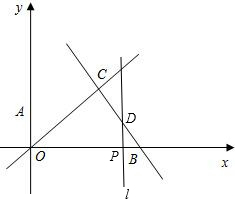
所以S=S△OCB-S△BPD=3-(3-x)2(或S=-x2+6x-6).
解得x=2,所以y=2,
所以C的坐标是(2,2)
(2)点A关于x轴的对称点A1为(0,-1),
直线A1C的解析式为y=
| 3 |
| 2 |
直线A1C与x轴的交点坐标是(
| 2 |
| 3 |
所以当点P运动到(
| 2 |
| 3 |
(3)∵C(2,2),B(3,0),
∴OB=3,
∴S△OCB=
| 1 |
| 2 |
当0<x≤2时,即l在点C左侧,

∵点P坐标为(x,0),
∴与直线y=x的交点D的坐标是(x,x),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当2<x<3时,即l在点C右侧,
∵P(x,0),
∴直线l与直线BC的交点D的坐标是(x,-2x+6),
∴S△BDP=
| 1 |
| 2 |
| 1 |
| 2 |

所以S=S△OCB-S△BPD=3-(3-x)2(或S=-x2+6x-6).
点评:本题主要考查对于一次函数图象的应用,以及平面展开最短路径的相关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
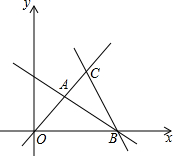 交于点A.
交于点A.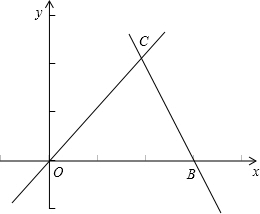 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.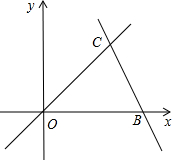 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.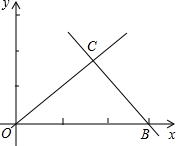 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直. 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.