题目内容
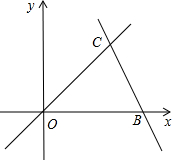 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.(1)求点C的坐标;
(2)设△OBC中位于直线l左侧部分的面积为s,写出s与x之间的函数关系式;
(3)在直角坐标系中画出(2)中函数的图象;
(4)当x为何值时,直线l平分△OBC的面积?
分析:(1)解两个函数解析式组成的方程组,就可以求出交点C的坐标.
(2)本题应分两种情况进行讨论,当直线l在C点的左侧和右侧两种情况.
(4)根据(3)中的函数解析式,就可以得到方程,解方程就可以解决.
(2)本题应分两种情况进行讨论,当直线l在C点的左侧和右侧两种情况.
(4)根据(3)中的函数解析式,就可以得到方程,解方程就可以解决.
解答: 解:(1)解方程组
解:(1)解方程组
,
消去y得:-2x+6=x,解得x=2,
把x=2代入y=x得:y=2,
所以
,
则C点的坐标是(2,2).
(2)过点C作CD⊥x轴于D,
当0<x≤2时,设直线l与OC交于点M,
则
=
,即
=
,
则PM=x,
则S=
OP•PM=
x2;
 当2<x<3时,△ODC的面积是
当2<x<3时,△ODC的面积是
×2×2=2,
∵OP=x,OD=2,则PD=x-2,CD=2,PN=-2x+6,
则梯形PNCD的面积为
×(-2x+6+2)×(x-2)=(-x+4)(x-2),
因而函数解析式是s=2+(-x+4)(x-2)=-x2+6x-6;
(4)当0<x≤2时,解方程
x2=
,解得x=
,
当2<x<3时,(3-x)2=
,
解得x=
(舍去),x=
(舍去).
总之,当x=
时,直线l平分△OBC的面积.
 解:(1)解方程组
解:(1)解方程组
|
消去y得:-2x+6=x,解得x=2,
把x=2代入y=x得:y=2,
所以
|
则C点的坐标是(2,2).
(2)过点C作CD⊥x轴于D,
当0<x≤2时,设直线l与OC交于点M,
则
| PM |
| CD |
| OP |
| OD |
| PM |
| 2 |
| x |
| 2 |
则PM=x,
则S=
| 1 |
| 2 |
| 1 |
| 2 |
 当2<x<3时,△ODC的面积是
当2<x<3时,△ODC的面积是| 1 |
| 2 |
∵OP=x,OD=2,则PD=x-2,CD=2,PN=-2x+6,
则梯形PNCD的面积为
| 1 |
| 2 |
因而函数解析式是s=2+(-x+4)(x-2)=-x2+6x-6;
(4)当0<x≤2时,解方程
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
当2<x<3时,(3-x)2=
| 3 |
| 2 |
解得x=
6-
| ||
| 2 |
6+
| ||
| 2 |
总之,当x=
| 3 |
点评:本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
相关题目
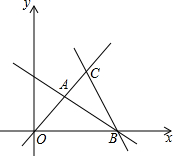 交于点A.
交于点A.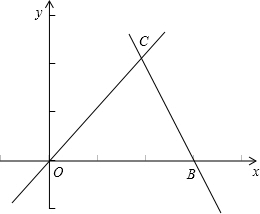 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.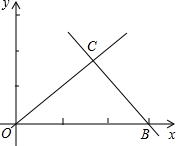 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直. 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.