题目内容
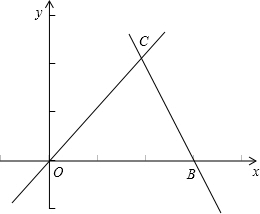 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式.
(3)当x为何值时,直线m平分△COB的面积?
分析:(1)由于C是直线OC、BC的交点,根据它们的解析式即可求出坐标,然后根据图象和交点坐标可以求出当x取何值时y1>y2;
(2)此小题有两种情况:①当0<x≤2,此时直线m左侧部分是△PQO,由于P(x,0)在OB上运动,所以PQ,OP都可以用x表示,所以s与x之间函数关系式即可求出;②当2<x<3,此时直线m左侧部分是四边形OPQC,可以先求出右边的△PQB的面积,然后即可求出左边的面积,而△PQO的面积可以和①一样的方法求出;
(3)利用(2)中的解析式即可求出x为何值时,直线m平分△COB的面积.
(2)此小题有两种情况:①当0<x≤2,此时直线m左侧部分是△PQO,由于P(x,0)在OB上运动,所以PQ,OP都可以用x表示,所以s与x之间函数关系式即可求出;②当2<x<3,此时直线m左侧部分是四边形OPQC,可以先求出右边的△PQB的面积,然后即可求出左边的面积,而△PQO的面积可以和①一样的方法求出;
(3)利用(2)中的解析式即可求出x为何值时,直线m平分△COB的面积.
解答:解:(1)依题意得
解方程组
,
得
,
∴C点坐标为(2,2);
根据图示知,当x>2时,y1>y2;
(2)如图,过C作CD⊥x轴于点D,
则D(2,0),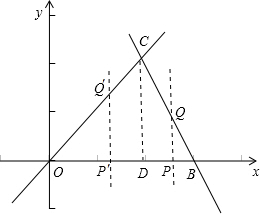
∵直线y2=-2x+6与x轴交于B点,
∴B(3,0),
①当0<x≤2,此时直线m左侧部分是△P′Q′O,
∵P′(x,0),
∴OP′=x,
而Q′在直线y1=x上,
∴P′Q′=x,
∴s=
x2(0<x≤2);
②当2<x<3,此时直线m左侧部分是四边形OPQC,
∵P(x,0),
∴OP=x,
∴PB=3-x,
而Q在直线y2=-2x+6上,
∴PQ=-2x+6,
∴S=S△BOC-S△PBQ=
×CD×OB-
×BP×PQ
=-x2+6x-6(2<x<3);
(3)直线m平分△BOC的面积,
则点P只能在线段OD,即0<x<2.
又∵△COB的面积等于3,
故
x2=3×
,
解之得x=
.
∴当x=
时,直线m平分△COB的面积.
解方程组
|
得
|
∴C点坐标为(2,2);
根据图示知,当x>2时,y1>y2;
(2)如图,过C作CD⊥x轴于点D,
则D(2,0),

∵直线y2=-2x+6与x轴交于B点,
∴B(3,0),
①当0<x≤2,此时直线m左侧部分是△P′Q′O,
∵P′(x,0),
∴OP′=x,
而Q′在直线y1=x上,
∴P′Q′=x,
∴s=
| 1 |
| 2 |
②当2<x<3,此时直线m左侧部分是四边形OPQC,
∵P(x,0),
∴OP=x,
∴PB=3-x,
而Q在直线y2=-2x+6上,
∴PQ=-2x+6,
∴S=S△BOC-S△PBQ=
| 1 |
| 2 |
| 1 |
| 2 |
=-x2+6x-6(2<x<3);
(3)直线m平分△BOC的面积,
则点P只能在线段OD,即0<x<2.
又∵△COB的面积等于3,
故
| 1 |
| 2 |
| 1 |
| 2 |
解之得x=
| 3 |
∴当x=
| 3 |
点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
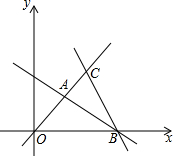 交于点A.
交于点A.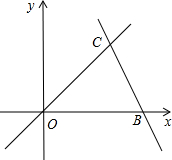 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.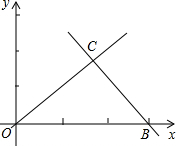 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.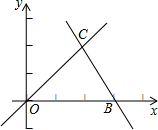 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.