题目内容
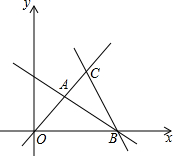
 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.(1)求点C的坐标.
(2)当x取何值时y1>y2?
(3)求△COB的面积.
分析:(1)解由两直线的解析式y=x和y=-2x+6所组成的方程组即可得到C点坐标;
(2)观察函数图象得到当x>3时,函数y1=x的图象都在函数y2=-2x+6的图象的上方,即有y1>y2;
(3)先利用y2=-2x+6求出B点坐标,得到OB的长,而△COB的OB边上的高等于C点的纵坐标,然后利用三角形面积公式即可.
(2)观察函数图象得到当x>3时,函数y1=x的图象都在函数y2=-2x+6的图象的上方,即有y1>y2;
(3)先利用y2=-2x+6求出B点坐标,得到OB的长,而△COB的OB边上的高等于C点的纵坐标,然后利用三角形面积公式即可.
解答:解:(1)解方程组
得
,
所以C点坐标为(2,2);
(2)当x>2时y1>y2;
(3)对于y=-2x+6,令y=0,则-2x+6=0,解得x=3,
所以B点坐标为(3,0),
所以△COB的面积=
×3×2=3.
|
|
所以C点坐标为(2,2);
(2)当x>2时y1>y2;
(3)对于y=-2x+6,令y=0,则-2x+6=0,解得x=3,
所以B点坐标为(3,0),
所以△COB的面积=
| 1 |
| 2 |
点评:本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.也考查了观察图象的能力.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 交于点A.
交于点A.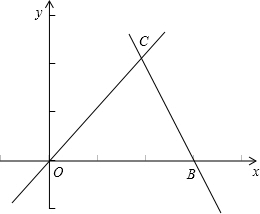 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.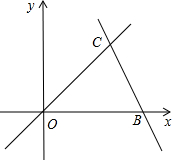 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.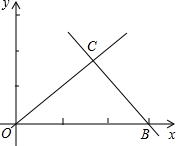 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.