题目内容
【题目】如图，一牧童在A处牧马，牧童家在B处，A、B距河岸的距离AC、BD的长分别为500米和700米，且C、D两地的距离为1600米，天黑前牧童从A点将马牵引到河边去饮水后再赶回家，那么牧童至少要走的距离是（ ）
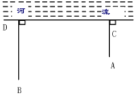
A. 2600米B. 2300米C. 2000米D. 1200米
【答案】C
【解析】
延长AC到E点，使AC=CE，连接BE交CD边于点M，过点E作EN⊥BD交BD的延长线于点N，则BE的长即为所求的长，即牧童最少要走的距离．由此求得BE的长即可.
延长AC到E点，使AC=CE，连接BE交CD边于点M，过点E作EN⊥BD交BD的延长线于点N，即可得四边形CENM是矩形，
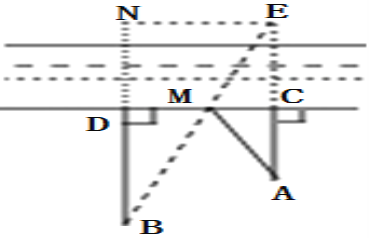
∴DN=EC，CD=NE，
连接BE交CD于M，此时BM+AM的值最小，为线段BE的长，
即BE为牧童要走的最短路程．
∵EN=CD=1600米，BN=DN+BD=BD+AC=500+700=1200（米），
∴在Rt△BNE中，BE=
（米）．
∴牧童至少要走2000米．
故选C.
练习册系列答案
相关题目
