题目内容
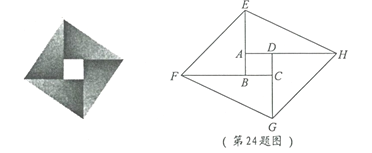
【题目】在一次课题学习中，老师让同学们合作编题，某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解：
如图，将矩形
的四边
、
、
、
分别延长至
、
、
、
，使得
，
，连接
，
，
，
.
(1) 求证：四边形
为平行四边形；
(2) 若矩形
是边长为1的正方形，且
，
，求
的长.
【答案】（1）证明见解析；（2）2
【解析】
试题分析：（1）易证AH=CF，结合已知条件由勾股定理可得EH=FG，同理可得EF=GH，从而得证.
（2）设AE=x，则BE=x+1，由
可得DH=x+1，AH=x+2,由
可求出结果.
试题分析：（1）在矩形ABCD中，AD=BC，∠BAD=∠BCD=90°
又∵BF=DH
∴AD+DH=BC+BF
即AH=CF
在RtΔAEH中，EH=
在RtΔCFG中，FG=
∵AE=CG
∴EH=FG
同理得：EF=HG
∴四边形EFGH为平行四边形．
（2）在正方形ABCD中，AB=AD=1
设AE=x,则BE=x+1
∵在RtΔBEF中，
∴BE=BF
∵BF=DH
∴DH=BE=x+1
∴AH=AD+DH=x+2
∵
∴AH=2AE
∴2+x=2x
∴x=2
即AE=2
练习册系列答案
相关题目
