Question

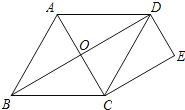
【题目】如图，菱形ABCD的对角线交于点O，点E是菱形外一点，DE∥AC，CE∥BD．

（1）求证：四边形DECO是矩形；

（2）连接AE交BD于点F，当∠ADB＝30°，DE＝2时，求AF的长度．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）根据菱形的性质求出∠DOC=90°，根据平行四边形和矩形的判定即可得出结论；

（2）求出DF=FO，解直角三角形求出OD，求出OF，根据勾股定理求出AF即可．

（1）∵四边形ABCD是菱形，∴AC⊥BD，即∠DOC=90°．

∵DE∥AC，CE∥BD，∴四边形DECO是平行四边形，∴四边形DECO是矩形；

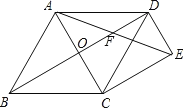
（2）∵四边形ABCD是菱形，∴AO=OC．

∵四边形DECO是矩形，∴DE=OC．

∵DE=2，∴DE=AO=2．

∵DE∥AC，∴∠OAF=∠DEF．

在△AFO和△EFD中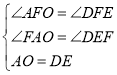，∵，∴△AFO≌△EFD（AAS），∴OF=DF．

在Rt△ADO中，tan∠ADB，∴，∴DO=2，∴FO，∴AF．