题目内容
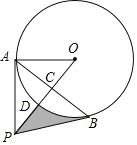
【题目】如图,点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 外一点.
外一点.![]() 切
切![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
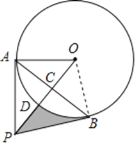
【答案】(1)见解析;(2)18![]() ﹣6π
﹣6π
【解析】
(1)连接OB,由垂径定理得OP垂直平分AB,进而证明△APO≌△BPO,得∠PAO=∠PBO,结合PA切⊙O于点A, 即可得到结论;
(2)先证△APB是等边三角形,设OB=x,则OP=2x,由勾股定理得OB=6,结合三角形的面积公式和扇形的面积公式,即可求解.
(1)连接OB,
∵OP⊥AB,OP经过圆心O,
∴AC=BC,
∴OP垂直平分AB,
∴AP=BP,
∵OA=OB,OP=OP,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,
∴∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB是⊙O的切线;
(2)∵PA切⊙O于点A, PB切⊙O于点B,
∴PA=PB,
∵∠APB=60°,
∴△APB是等边三角形,
∴PB=AB=6![]() ,
,
在Rt△OPB中,
∵∠OPB=∠OPA=![]() ∠APB=30°,
∠APB=30°,
∴OP=2OB,∠POB=60°,
设OB=x,则OP=2x,
由勾股定理得: x2+(6![]() )2=(2x)2
)2=(2x)2
∵x>0
∴x=6 , 即OB=6,
∴S△OPB=![]() ×BP×OB=
×BP×OB=![]() ×6
×6![]() ×6=18
×6=18![]() ,S扇DOB=
,S扇DOB=![]() =6π,
=6π,
∴S阴影=S△OPB﹣S扇DOB=18![]() ﹣6π.
﹣6π.

练习册系列答案
相关题目