题目内容
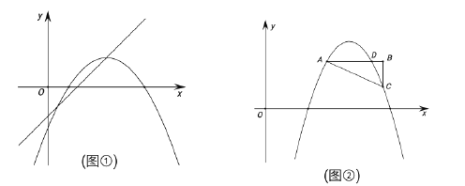
【题目】如图①,将抛物线![]() 平移到顶点恰好落在直线
平移到顶点恰好落在直线![]() 上,并设此时抛物线顶点的横坐标为
上,并设此时抛物线顶点的横坐标为![]() .
.
(1)求抛物线的解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
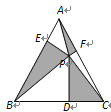
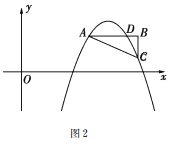
(2)如图②,![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() ,
,![]() 轴,
轴,![]() ,
,![]() .
.
①求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
②若![]() 的面积为1,当
的面积为1,当![]() 时,
时,![]() 的最大值为-3,求
的最大值为-3,求![]() 的值.
的值.
【答案】(1)![]() ; (2)①
; (2)①![]() ;②
;②![]() 的值为0或
的值为0或![]() .
.
【解析】
(1)根据抛物线顶点的横坐标为![]() ,代入
,代入![]() 可得纵坐标,从而可求出抛物线的解析式;
可得纵坐标,从而可求出抛物线的解析式;
(2) ①设![]() ,则
,则![]() ,表示出点B,C,D的坐标, 根据点
,表示出点B,C,D的坐标, 根据点![]() 在抛物线上,把点C的坐标代入抛物线即可用a表示出t的值,再根据三角形的面积公式可求出;
在抛物线上,把点C的坐标代入抛物线即可用a表示出t的值,再根据三角形的面积公式可求出;
②根据![]() 的面积为1求出a的值,表示出抛物线的解析式,分三种情况可求出m的值.
的面积为1求出a的值,表示出抛物线的解析式,分三种情况可求出m的值.
(1)因为抛物线的顶点位于直线![]() 上,且横坐标为
上,且横坐标为![]() ,
,
所以抛物线的顶点坐标为![]() .
.
因此抛物线的解析式为![]() ;
;
(2)①如图所示.
因为![]() 轴,且
轴,且![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.
设![]() ,则
,则![]() ,
,
所以![]() 点的坐标为
点的坐标为![]() .
.
![]() 点的坐标为
点的坐标为![]() .
.
又点![]() 在抛物线
在抛物线![]() 上,
上,
所以![]() ,
,
整理,得![]() .
.
解得![]() (舍去),
(舍去),![]() .
.
所以![]() .
.
②若![]() 的面积为1,则
的面积为1,则![]() ,解得
,解得![]() .
.
所以抛物线的解析式为![]() .
.
分三种情况考虑:
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
整理,得![]() ,
,
此方程没有实数根;
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
解得![]() ;
;
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
整理,得![]() ,
,
解得![]() (舍去),
(舍去),![]() .
.
综上所述,![]() 的值为0或
的值为0或![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目