题目内容
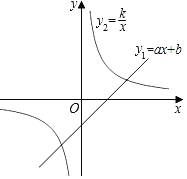
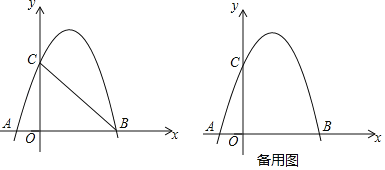
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
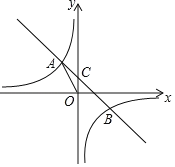
【答案】(1)﹣10;(2)B(5,﹣2),y=﹣x+3;(3)P点的坐标为(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)作AD⊥y轴于D,根据正切函数,可得AD的长,得到A的坐标,根据待定系数法,可得k的值;
(2)根据题意即可求得B点的坐标,然后根据待定系数法即可求得直线AB的解析式;
由直线AB为y=﹣x+3可知,C(0,3);
(3)先求出C点坐标,即可求得S△AOB,设P(0,t),根据S△PBC=2S△AOB,即可求出t值,进而求得P点坐标.
(1)作AD⊥y轴于D,
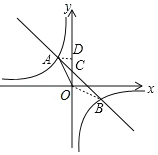
∵点A的坐标为(m,5),
∴OD=5
∵tan∠AOC![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AD=2,
∴A(﹣2,5).
∵在反比例函数y![]() (k为常数,k≠0)的图象上,
(k为常数,k≠0)的图象上,
∴k=﹣2×5=﹣10;
故答案为:-10
(2)∵反比例函数为y![]() ,
,
∴B(5,﹣2).
∵A、B在一次函数y=ax+b的图象上,
∴![]()
解得![]() ,
,
∴直线AB的解析式为y=﹣x+3;
故答案为:B(5,﹣2),y=﹣x+3
(3)连接OB,

由直线AB为y=﹣x+3可知,C(0,3).
∵S△AOB=S△AOC+S△BOC![]() 3×2
3×2![]() 3×5
3×5![]() ,
,
∵P是y轴上一点,
∴设P(0,t),
∴S△PBC![]() |t﹣3|×5
|t﹣3|×5![]() |t﹣3|.
|t﹣3|.
∵S△PBC=2S△AOB,
∴![]() |t﹣3|=2
|t﹣3|=2![]() ,
,
∴t![]() 或t
或t![]() ,
,
∴P点的坐标为(0,![]() )或(0,
)或(0,![]() ).
).

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目