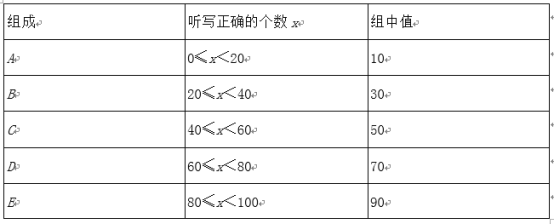
题目内容
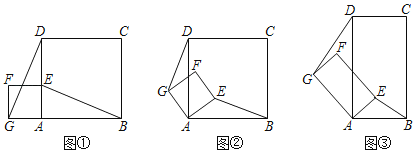
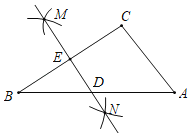
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,①△BCE是等边三角形,②DE=BF,③△ABC≌△CFD,④四边形BEDF是平行四边形.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由直角三角形的性质和旋转的性质可得![]() ,
,![]() ,
,![]() ,
,![]() ,可判断①②;由“
,可判断①②;由“![]() ”可证
”可证![]() ,可判断③,延长
,可判断③,延长![]() 交
交![]() 于点
于点![]() ,可证
,可证![]() ,由一组对边平行且相等可证四边形
,由一组对边平行且相等可证四边形![]() 是平行四边形,即可判断④,即可求解.
是平行四边形,即可判断④,即可求解.
∵点F是边AC中点,∴CF=BF=AF![]() AC.
AC.
∵∠BCA=30°,∴BA![]() AC,∴BF=AB=AF=CF,∴∠FCB=∠FBC=30°.
AC,∴BF=AB=AF=CF,∴∠FCB=∠FBC=30°.
∵将△ABC绕点C顺时针旋转60°得到△DEC,∴∠BCE=∠ACD=60°,CB=CE,∠DEC=∠ABC=90°,AB=DE,∴△BCE是等边三角形,DE=BF,故①②正确;
∵CD=AC,AB=CF,∴Rt△ABC≌Rt△CFD(HL),故③正确;
延长BF交CE于点G,则∠BGE=∠GBC+∠BCG=90°,
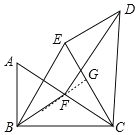
∴∠BGE=∠DEC,∴BF∥ED,∴四边形BEDF是平行四边形,故④正确.
故选:D.

练习册系列答案
相关题目