题目内容
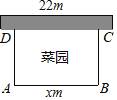
【题目】如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(矩形ABCD),墙长为22m,这个矩形的长AB=xm,菜园的面积为Sm2,且AB>AD.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围.
(2)若要围建的菜园为100m2时,求该莱园的长.
(3)当该菜园的长为多少m时,菜园的面积最大?最大面积是多少m2?
【答案】(1)S=﹣![]() x2+15x,10<x≤22;(2)菜园的长为20m;(3)该菜园的长为15m时,菜园的面积最大,最大面积是112.5m2.
x2+15x,10<x≤22;(2)菜园的长为20m;(3)该菜园的长为15m时,菜园的面积最大,最大面积是112.5m2.
【解析】
(1)根据矩形的面积公式即可得结论;
(2)根据题意列一元二次方程即可求解;
(3)根据二次函数的顶点式即可求解.
解:(1)由题意可知:AD=![]() (30﹣x)
(30﹣x)
∴S=ABAD
=x×![]() (30﹣x)
(30﹣x)
=﹣![]() x2+15x
x2+15x
自变量x的取值范围是10<x≤22.
(2)当S=100时,﹣![]() x2+15x=100
x2+15x=100
解得x1=10,x2=20,
又10<x≤22.
∴x=20,
答:该菜园的长为20m.
(3)∵S=﹣![]() x2+15x
x2+15x
=﹣![]() (x﹣15)2+
(x﹣15)2+![]()
又10<x≤22.
∴当x=15时,S取得最大值,最大值为112.5.
答:该菜园的长为15m时,菜园的面积最大,最大面积是112.5m2.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目