题目内容
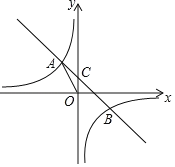
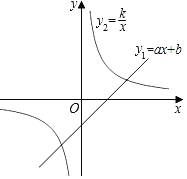
【题目】如图,已知一次函数y1=ax+b(a≠0)与反比例函数y2=![]() (k>0),两函数图象交于(4,1),(﹣2,n)两点.
(k>0),两函数图象交于(4,1),(﹣2,n)两点.
(1)求a,k的值;
(2)若y2>y1>0,求x的取值范围.
【答案】(1)a=![]() ,k=4;(2)2<x<4.
,k=4;(2)2<x<4.
【解析】
(1)先把(4,1)代入y2=![]() 求出k确定反比例函数解析式,再利用反比例函数解析式求出n,然后根据待定系数法求一次函数解析式,即可求出a的值;
求出k确定反比例函数解析式,再利用反比例函数解析式求出n,然后根据待定系数法求一次函数解析式,即可求出a的值;
(2)在第一象限内,写出反比例函数图像在一次函数图像上方所对应的自变量的范围即可.
解:(1)把(4,1)代入y2=![]() 得k=4×1=4,
得k=4×1=4,
∴反比例函数解析式为y2=![]() ,
,
把(﹣2,n)代入y2=![]() 得﹣2n=4,解得n=﹣2,
得﹣2n=4,解得n=﹣2,
把(4,1),(﹣2,﹣2)代入y1=ax+b得![]() ,解得
,解得 ,
,
∴一次函数解析式为y1=![]() x﹣1,
x﹣1,
∴a=![]() ,k=4;
,k=4;
(2)当![]() x﹣1=0,解得x=2,则一次函数y1=ax+b(a≠0)图像与x轴的交点为(2,0),根据函数图像可得:当2<x<4时,y2>y1>0.
x﹣1=0,解得x=2,则一次函数y1=ax+b(a≠0)图像与x轴的交点为(2,0),根据函数图像可得:当2<x<4时,y2>y1>0.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
【题目】在某项比赛中,已知不同小组的甲、乙两队的五次预选赛成绩(每次比赛的成绩为0分,10分,20分三种情况)分别如下列不完整的统计表及条形统计图所示.
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 | x | 20 |
乙队五次预选赛成绩条形统计图
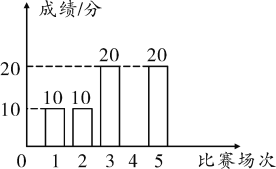
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)求出乙第四次预选赛的成绩;
(2)求甲队成绩的平均数及x的值;
(3)从甲、乙两队前3次比赛中随机各选择一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.