题目内容
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
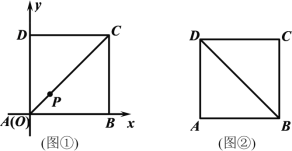
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
【答案】(1) P![]() (2)m,n需满足的条件是m+n<1且m>0且n>0
(2)m,n需满足的条件是m+n<1且m>0且n>0
【解析】
(1)根据正方形的性质得出m=n即可。
(2) 过点![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() , 延长
, 延长![]() 交对角线
交对角线![]() 于点
于点![]() .,根据当点
.,根据当点![]() 的内部时,得出
的内部时,得出![]() ,所以
,所以![]() ,从而得出结论
,从而得出结论
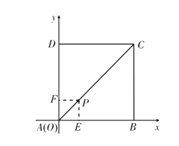
(1)如图,过点![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]()
![]() 到边
到边![]() 的距离分别为
的距离分别为![]()
![]() .
.
![]() .
.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() 平分
平分![]() . .
. .
![]() 点
点![]() 在对角线
在对角线![]() 上,
上,
![]()
![]()
(2) 如图,过点![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,
,
![]() 到边
到边![]() 的距高分別カ
的距高分別カ![]() ,
,
![]() .
.
在正方形![]() 中,
中,![]() .
.
![]() .
.
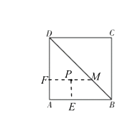
四辺形![]() 为矩形.
为矩形.
![]() .
.
若点![]() 的内部,
的内部,
则延长![]() 交对角线
交对角线![]() 于点
于点![]() .
.
在![]() 中,
中,![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() .
.
即![]() .
.
又![]() ,
,
![]() 需满足的条件是
需满足的条件是![]() 且
且 ![]()

练习册系列答案
相关题目