ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐyΘΫaΘ®x©¹hΘ©2+kΘ®aΓΌ0Θ©ΒΡΆΦœσ «≈ΉΈοœΏΘ§Ε®“ε“Μ÷÷±δΜΜΘ§œ»Ής’βΧθ≈ΉΈοœΏΙΊ”Ύ‘≠ΒψΕ‘≥ΤΒΡ≈ΉΈοœΏyΓδΘ§‘ΌΫΪΒΟΒΫΒΡΕ‘≥Τ≈ΉΈοœΏyΓδœρ…œΤΫ“ΤmΘ®mΘΨ0Θ©ΗωΒΞΈΜΘ§ΒΟΒΫ–¬ΒΡ≈ΉΈοœΏymΘ§Έ“Ο«≥ΤymΫ–ΉωΕΰ¥ΈΚ· ΐyΘΫaΘ®x©¹hΘ©2+kΘ®aΓΌ0Θ©ΒΡmΫΉ±δΜΜΘ°
Θ®1Θ©“―÷ΣΘΚΕΰ¥ΈΚ· ΐyΘΫ2Θ®x+2Θ©2+1Θ§ΥϋΒΡΕΞΒψΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣΓΓ ΓΓΘ§’βΗω≈ΉΈοœΏΒΡ2ΫΉ±δΜΜΒΡ±μ¥ο ΫΈΣΓΓ ΓΓΘ°
Θ®2Θ©»τΕΰ¥ΈΚ· ΐMΒΡ6ΫΉ±δΜΜΒΡΙΊœΒ ΫΈΣy6ΓδΘΫΘ®x©¹1Θ©2+5Θ°
ΔΌΕΰ¥ΈΚ· ΐMΒΡΚ· ΐ±μ¥ο ΫΈΣΓΓ ΓΓΘ°
ΔΎ»τΕΰ¥ΈΚ· ΐMΒΡΕΞΒψΈΣΒψAΘ§”κx÷αœύΫΜΒΡΝΫΗωΫΜΒψ÷–Ήσ≤ύΫΜΒψΈΣΒψBΘ§‘Ύ≈ΉΈοœΏy6ΓδΘΫΘ®x©¹1Θ©2+5…œ «Ζώ¥φ‘ΎΒψPΘ§ ΙΒψP”κ÷±œΏABΒΡΨύάκΉνΕΧΘ§»τ¥φ‘ΎΘ§«σ≥ω¥Υ ±ΒψPΒΡΉχ±ξΘ°
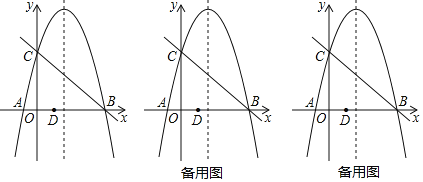
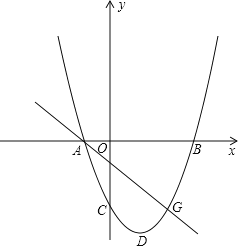
Θ®3Θ©≈ΉΈοœΏyΘΫ©¹3x2©¹6x+1ΒΡΕΞΒψΈΣΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§ΗΟ≈ΉΈοœΏΒΡmΫΉ±δΜΜΒΡΕΞΒψΈΣΒψCΘ°»τΓςABC «“‘ABΈΣ―ϋΒΡΒ»―ϋ»ΐΫ«–Έ,«κ÷±Α¥–¥≥ωmΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®2Θ§©¹1Θ©Θ§yΘΫ©¹2Θ®x©¹2Θ©2©¹1ΘΜΘ®2Θ©¥φ‘ΎΘ§ΒψPΘ®![]() Θ§
Θ§![]() Θ©Θ§Θ®3Θ©8+
Θ©Θ§Θ®3Θ©8+![]() Μρ8©¹
Μρ8©¹![]() Μρ8Μρ2Θ°
Μρ8Μρ2Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©‘≠Εΰ¥ΈΚ· ΐΒΡΕΞΒψΈΣΘ®-2Θ§1Θ©Θ§‘ρΕΞΒψΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣΘ®2Θ§-1Θ©Θ§Φ¥Ω…«σΫβΘΜΘ®2Θ©ΔΌ6ΫΉ±δΜΜΒΡΙΊœΒ ΫΕ‘”ΠΒΡΚ· ΐΕΞΒψΈΣΘΚΘ®1Θ§-1Θ©Θ§‘ρΚ· ΐMΒΡΕΞΒψΈΣΘΚΘ®-1Θ§1Θ©Θ§Φ¥Ω…«σΫβΘΜΔΎDP =![]() PH=
PH=![]() Θ®x2-2x+6-x-2Θ©=
Θ®x2-2x+6-x-2Θ©=![]() Θ®x2-3x+4Θ©Θ§Φ¥Ω…«σΫβΘΜ
Θ®x2-3x+4Θ©Θ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©ΒψAΘ®-1Θ§4Θ©ΓΔΒψBΘ®0Θ§1Θ©Θ§≈ΉΈοœΏΒΡmΫΉ±δΜΜΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚy=3Θ®x-1Θ©2-4+mΘ§Ι ΒψCΘ®1Θ§m-4Θ©Θ§Φ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©‘≠Εΰ¥ΈΚ· ΐΒΡΕΞΒψΈΣΘ®©¹2Θ§1Θ©Θ§‘ρΕΞΒψΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣΘ®2Θ§©¹1Θ©Θ§
‘ρ’βΗω≈ΉΈοœΏΒΡ2ΫΉ±δΜΜΒΡ±μ¥ο ΫΘΚyΘΫ©¹2Θ®x©¹2Θ©2©¹1Θ§
Ι ¥πΑΗΈΣΘΚΘ®2Θ§©¹1Θ©Θ§yΘΫ©¹2Θ®x©¹2Θ©2©¹1ΘΜ
Θ®2Θ©ΔΌ6ΫΉ±δΜΜΒΡΙΊœΒ ΫΕ‘”ΠΒΡΚ· ΐΕΞΒψΈΣΘΚΘ®1Θ§©¹1Θ©Θ§‘ρΚ· ΐMΒΡΕΞΒψΈΣΘΚΘ®©¹1Θ§1Θ©Θ§
‘ρΤδ±μ¥ο ΫΈΣΘΚyΘΫ©¹Θ®x+1Θ©2+1Θ§
Ι ¥πΑΗΈΣΘΚyΘΫ©¹Θ®x+1Θ©2+1ΘΜ
ΔΎ¥φ‘ΎΘ§άμ”…ΘΚ
yΘΫ©¹Θ®x+1Θ©2+1Θ§ΝνyΘΫ0Θ§‘ρxΘΫ©¹2Μρ0Θ§
Ι ΒψBΘ®©¹2Θ§0Θ©Θ§ΕχΒψAΘ®©¹1Θ§1Θ©Θ§
ΫΪΒψAΓΔBΒΡΉχ±ξ¥ζ»κ“Μ¥ΈΚ· ΐ±μ¥ο ΫΘΚyΘΫkx+bΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Ι ÷±œΏABΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚyΘΫx+2Θ§
y6ΓδΘΫΘ®x©¹1Θ©2+5ΘΫx2©¹2x+6Θ§
»γœ¬ΆΦΘ§ΙΐΒψPΉςPDΓΆABΫΜ”ΎΒψDΘ§Ι ΒψPΉςy÷αΒΡΤΫ––œΏΫΜAB”ΎΒψHΘ§
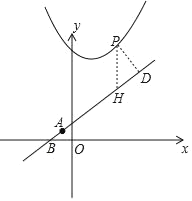
ΓΏ÷±œΏABΒΡ«ψ–±Ϋ«ΈΣ45ΓψΘ§‘ρDPΘΫ![]() PHΘ§
PHȧ
…ηΒψPΘ®xΘ§x2©¹2x+6Θ©Θ§‘ρΒψHΘ®xΘ§x+2Θ©Θ§
DPΘΫ![]() PHΘΫ
PHΘΫ![]() Θ®x2©¹2x+6©¹x©¹2Θ©ΘΫ
Θ®x2©¹2x+6©¹x©¹2Θ©ΘΫ![]() Θ®x2©¹3x+4Θ©Θ§
Θ®x2©¹3x+4Θ©Θ§
ΓΏ![]() ΘΨ0Θ§Ι DP”–Ήν–Γ÷ΒΘ§¥Υ ±xΘΫ
ΘΨ0Θ§Ι DP”–Ήν–Γ÷ΒΘ§¥Υ ±xΘΫ![]() Θ§
Θ§
Ι ΒψPΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©≈ΉΈοœΏyΘΫ©¹3x2©¹6x+1ΒΡΕΞΒψΈΣΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§
‘ρΒψAΘ®©¹1Θ§4Θ©ΓΔΒψBΘ®0Θ§1Θ©Θ§
≈ΉΈοœΏΒΡmΫΉ±δΜΜΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚyΘΫ3Θ®x©¹1Θ©2©¹4+mΘ§
Ι ΒψCΘ®1Θ§m©¹4Θ©Θ§
‘ρAB2ΘΫ10Θ§AC2ΘΫ4+Θ®m©¹8Θ©2Θ§BC2ΘΫ1+Θ®m©¹5Θ©2Θ§
Β±ABΘΫAC ±Θ§10ΘΫ4+Θ®m©¹8Θ©2Θ§ΫβΒΟΘΚmΘΫ8![]() ΘΜ
ΘΜ
Β±ABΘΫBC ±Θ§Ά§άμΩ…ΒΟΘΚmΘΫ8Μρ2Θ§
Ι mΒΡ÷ΒΈΣΘΚ8+![]() Μρ8©¹
Μρ8©¹![]() Μρ8Μρ2Θ°
Μρ8Μρ2Θ°