题目内容
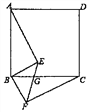
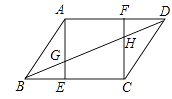
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB= ![]() .
.
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴∠CDF=∠ABE,DC=AB= ![]() ,
,
∵tan∠ABE=2,
∴tan∠CDF=2,∵CF⊥AD,
∴△CFD是直角三角形,
∴ ![]() =2,设DF=x,则CF=2x,
=2,设DF=x,则CF=2x,
在Rt△CFD中,由勾股定理可得(2x)2+x2=( ![]() )2,
)2,
解得x=2或x=﹣2(舍去),
∴CF=4;
(2)解:证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥BC,CF⊥AD,∴AE⊥AD,CF⊥BC,
∴∠GAD=∠HCB=90°,
∴△AGD≌△CHB,
∴BH=DG,
∴BG=DH.
【解析】(1)由平行四边形的性质,结合三角函数的定义,在Rt△CFD中,可求得CF=2DF,再利用勾股定理可求得CF的长。
(2)利用平行四边形的性质结合条件可证得△AGD≌△CHB,则可求得BH=DG,从而可证得BG=DH。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目