题目内容
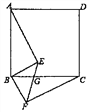
【题目】如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G.
(1)求证：AE=CF；
(2)若∠ABE=55°，求∠EGC的大小．
【答案】（1）证明见解析；（2）80°.
【解析】试题分析：（1）利用△AEB≌△CFB来求证AE=CF．
（2）利用角的关系求出∠BEF和∠EBG，∠EGC=∠EBG+∠BEF求得结果．
试题解析：（1）证明：∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC，
∵BE⊥BF，
∴∠FBE=90°，
∵∠ABE+∠EBC=90°，∠CBF+∠EBC=90°，
∴∠ABE=∠CBF，
在△AEB和△CFB中，
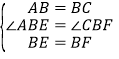
∴△AEB≌△CFB（SAS），
∴AE=CF．
（2）∵BE⊥BF，
∴∠FBE=90°，
又∵BE=BF，
∴∠BEF=∠EFB=45°，
∵四边形ABCD是正方形，
∴∠ABC=90°，
又∵∠ABE=55°，
∴∠EBG=90°﹣55°=35°，
∴∠EGC=∠EBG+∠BEF=45°+35°=80°．
阅读快车系列答案
【题目】某仓库本周运进货物件数和运出货物件数如下表：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
运进货物件数 | 5 | a | 5 | 5 | b | 5 | 5 |
运出货物件数 | 12 | 2a | 8 | 0 | b﹣5 | 5 | 10 |
（1）如果用正数表示运进货物件数，负数表示运出货物件数，请你分别表示出周二、周五当天进出货物后变化的量；
（2）若经过一周的时间，仓库货物总量相比上周末库存量减少了5件，求a的值；
（3）若本周运进货物总件数比运出货物件数的一半多15件，本周运进货物总件数比上周减少
，而本周运出货物总件数比上周多
，这两周内，该仓库货物共增加了3件，求a、b的值．
【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如下表（注：水费按月份结算，
表示立方米）：
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注：水费按月结算 | |
例：若某户居民
月份用水
，应收水费为
（元）．
请根据上表的内容解答下列问题：
填空：若该户居民
月份用水
，则应收水费________元；
若该户居民
月份用水
（其中
），则应收水费多少元？（用含
的表示，并化简）
若该户居民
，
两个月共用水
（月份用水量超过了月份），设月份用水
，求该户居民，两个月共交水费多少元？（用含
的表示，并化简）
