题目内容
【题目】在△ABC中,∠A=![]() ∠B=
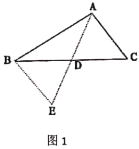
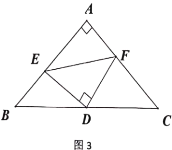
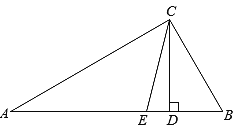
∠B=![]() ∠ACB,CD是△ABC的高,CE是∠ACB的角平分线,求∠DCE的度数。
∠ACB,CD是△ABC的高,CE是∠ACB的角平分线,求∠DCE的度数。
【答案】15°
【解析】
试题根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,然后根据直角三角形两锐角互余求出∠ACD,最后根据角平分线的定义求出∠ACE即可.
试题解析:∵∠A=![]() ∠B=
∠B=![]() ∠ACB,设∠A=x,∴∠B=2x,∠ACB=3x,
∠ACB,设∠A=x,∴∠B=2x,∠ACB=3x,
∵∠A+∠B+∠ACB=180°,∴x+2x+3x=180°,
解得x=30°,∴∠A=30°,∠ACB=90°,
∵CD是△ABC的高,∴∠ADC=90°,∴∠ACD=90°-30°=60°,
∵CE是∠ACB的角平分线,∴∠ACE=![]() ×90°=45°,
×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
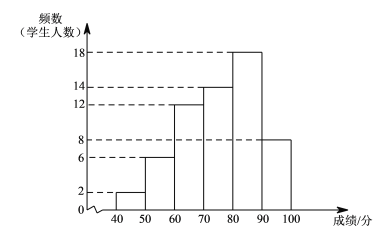
![]() .A课程成绩在
.A课程成绩在![]() 这一组是:
这一组是:
70 71 71 71 76 76 77 78 ![]()
![]() 79 79 79
79 79 79 ![]()
![]() .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过![]() 分的人数.
分的人数.