题目内容
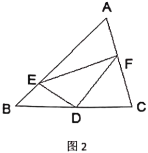
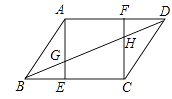
【题目】如图,△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角的平分线,CE⊥AE于点E. 求证:四边形ADCE是矩形.
【答案】证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD= ![]() ∠BAC,
∠BAC,
∵AE是∠BAC的外角的平分线,
∴∠CAE=∠FAE= ![]() ∠FAC,
∠FAC,
∵∠BAC+∠FAC=180°,
∴∠DAC+∠EAC= ![]() ×180°=90°,
×180°=90°,
即∠DAE=90°,
∵CE⊥AE,
∴∠AEC=90°,
∵AB=AC,
∴∠B=∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠B+∠ACB=∠FAE+∠CAE,
∴∠FAE=∠B,
∴AE∥BC,
∴∠AEC+∠ECB=180°,
∴∠ECB=90°,
∴∠DAE=∠AEC=∠ECB=90°,
∴四边形ADCE是矩形.
【解析】由角平分线定义得:∠BAD=∠CAD= ![]() ∠BAC和∠CAE=∠FAE=
∠BAC和∠CAE=∠FAE= ![]() ∠FAC,则∠DAE=90°,再证明∠AEC=∠ECB=90°,由三个角是直角的四边形是矩形得出结论.
∠FAC,则∠DAE=90°,再证明∠AEC=∠ECB=90°,由三个角是直角的四边形是矩形得出结论.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目