题目内容
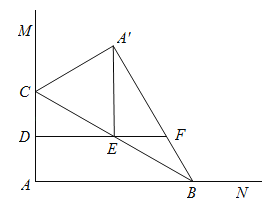
【题目】如图,已知点A是反比例函数 ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 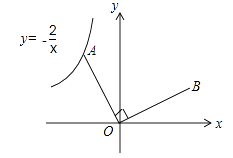
【答案】![]()
【解析】∵点A是反比例函数 ![]() 的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
∴AC=n,OC=﹣m,
∴∠ACO=∠ADO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中,
∵∠ACO=∠ODB,∠CAO=∠BOD,AO=BO,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=﹣m,
∴B(n,﹣m),
∵mn=﹣2,
∴n(﹣m)=2,
∴点B所在图象的函数表达式为 ![]() ,
,
故答案为: ![]() .
.
过A作AC⊥x轴于C,过B作BD⊥x轴于D,根据旋转的性质得出AO=BO,再证明∠ACO=∠ODB,∠CAO=∠BOD,可得出OC=BD,AC=OD,然后求出mn的值即可得出点B所在图象的函数解析式。

练习册系列答案
相关题目