题目内容
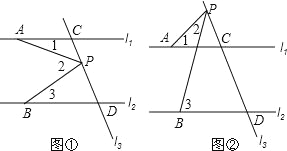
【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
【答案】(1)∠2=∠1+∠3;(2)不成立,应为∠3=∠1+∠2,证明见解析.
【解析】试题分析:(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,故可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)设PB与l1交于点F,根据l1∥l2可知∠3=∠PFC.在△APF中,根据∠PFC是△APF的一个外角即可得出结论.
试题解析:解:(1)∠2=∠1+∠3.证明如下:
如图①,过点P作PE∥l1.∵l1∥l2,∴PE∥l2,∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,∴∠2=∠1+∠3;
(2)上述结论不成立,新的结论:∠3=∠1+∠2.证明如下:
如图②,设PB与l1交于点F.∵l1∥l2,∴∠3=∠PFC.
在△APF中,∵∠PFC是△APF的一个外角,∴∠PFC=∠1+∠2,即∠3=∠1+∠2.

【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).



