Question

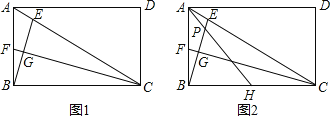
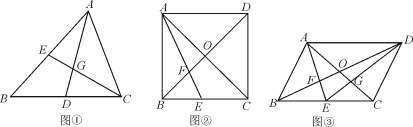
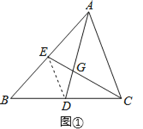
【题目】（1）证明推断：如图①，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：．

（2）类比探究：如图②，在正方形ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F，若AB＝6，求OF的长；

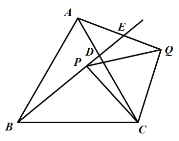
（3）拓展运用：若正方形ABCD变为□ABCD，如图③，连结DE交AC于点G，若四边形OFEG的面积为，求□ABCD的面积．

Answer 1

【答案】（1）见解析；（2）；（3）6

【解析】

（1）如图①，连结ED，根据三角形的中位线定理可得DE∥AC，DE＝AC，进而可得△DEG∽△ACG，然后根据相似三角形的性质和比例的性质即可证得结论；

（2）根据正方形的性质可得AD∥BC，BE＝BC＝AD，BO＝BD，进而可得△BEF∽△DAF，于是，进一步即可推得OF与BD的关系，而BD易求，则OF可得；

（3）如图③，连接OE，由（2）题的结论可推出，进而可得△BEF与△OEF的面积比为2，同理可得△CEG与△OEG的面积比，进一步即可求出△BOC的面积，而S□ABCD＝4 S△BOC，问题即得解决．

证明：（1）如图①，连结ED，

在△ABC中，∵D，E分别是边BC，AB的中点，

∴DE∥AC，DE＝AC，

∴△DEG∽△ACG，

∴，

∴，

∴；

（2）解：如图②．

∵四边形ABCD为正方形，E为边BC的中点，

∴AD∥BC，BE＝BC＝AD，BO＝BD，

∴△BEF∽△DAF，

∴，

∴BF＝DF，

∴BF＝BD．

∵BO＝BD，

∴OF＝OB﹣BF＝BD﹣BD＝BD．

∵正方形ABCD中，AB＝6，

∴BD＝6，

∴OF＝；

（3）如图③，连接OE．

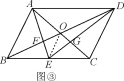
由（2）题知，BF＝BD，OF＝BD，

∴．

∵△BEF与△OEF的高相同，

∴△BEF与△OEF的面积比为2，

同理，△CEG与△OEG的面积比＝2，

∴S△CEG+S△BEF＝2（S△OEG+S△OEF）＝2×＝1，

∴S△BOC＝，

∴S□ABCD＝4 S△BOC＝4×＝6．