��Ŀ����
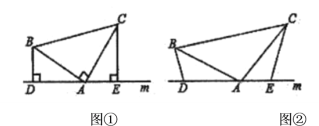
����Ŀ��ͼ�α任�е���ѧ�������龳���ڿ����ϣ���ȤѧϰС���һ����ѧ�������������̽������Rt��ABC�У���ACB��90������A��30������D��AB���е㣬����CD��̽�����֣�
��1����ͼ�٣�BC��BD��������ϵ�� ��
��2����ͼ�٣�CD��AB��������ϵ�� ����˵�����ɣ�
������֤��
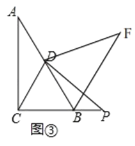
��3����ͼ�ڣ���P���߶�CB��һ���㣨��P�����B��C�غϣ�������DP�����߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF������BF�������BF��BP��BD����֮���������ϵ����֤����Ľ��ۣ�
��չ���죺
��4������P���߶�CB�ӳ�����һ���㣬���գ�3���е�����������ͼ���в�ȫͼ��ֱ��д��BF��BP��BD����֮���������ϵ��

���𰸡���1��BC=BD����2��CD=![]() AB����3��BF+BP��BD��֤������������4����ͼ��������BF��BD+BP��
AB����3��BF+BP��BD��֤������������4����ͼ��������BF��BD+BP��
��������
��1������30��ֱ�������ε����ʺ��е�Ķ��壬���ɵõ��𰸣�
��2������30��ֱ�������ε����ʺ��е�Ķ��壬֤����DBC�ǵȱ������Σ����ɵõ��𰸣�
��3��ͬ��2���ķ����ó�BC=BD�����ó���BCD�ǵȱ������Σ������жϳ���DCP����DBF���ó�CP=BF���ɵó����ۣ�
��4��ͬ��3���ķ����ó�BC=BD�����ó���BCD�ǵȱ������Σ������жϳ���DCP�ա�DBF���ó�CP=BF���ɵó����ۣ�
�⣺��1������Rt��ABC�У���ACB��90������A��30����
��![]() ��
��
�ߵ�DʱAB���е㣬
��![]() ��
��
��BC=BD��
�ʴ�Ϊ��BC=BD��
��2��CD=![]() AB��
AB��
���ɣ��ߡ�ACB��90������A��30����
���CBA��60����BC��![]() AB��
AB��
�ߵ�D��AB���е㣬
��BC��BD��
���DBC�ǵȱ������Σ�
��CD=BC��
��BC��![]() AB��
AB��
��CD=![]() AB��
AB��
�ʴ�Ϊ��CD��![]() AB��
AB��
��3��BF+BP��BD��
���ɣ��ɣ�2��֪ ��DBC�ǵȱ������Σ�
���CDB��60����DC��DB��
���߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF��
���PDF��60����DP��DF��
���CDB����PDB����PDF����PDB��
���CDP����BDF��
���DCP�ա�DBF��
��CP��BF��
��CP+BP��BC��
��BF+BP��BC��
��BC��BD��
��BF+BP��BD��
��4����ͼ�ۣ�BF=BD+BP��
���ɣ�����ACB=90������A=30����
���CBA=60����BC=![]() AB��
AB��
�ߵ�D��AB���е㣬
��BC=BD��
���DBC�ǵȱ������Σ�
���CDB=60����DC=DB��
���߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF��
���PDF=60����DP=DF��
���CDB+��PDB=��PDF+��PDB��
���CDP=��BDF��
�ڡ�DCP�͡�DBF�У�
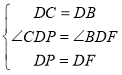 ��
��
���DCP�ա�DBF��
��CP=BF��
��CP=BC+BP��
��BF=BC+BP��
��BC=BD��
��BF=BD+BP��

����Ŀ�����꼶�ס�������ͬѧ��ĩ���Եijɼ�(��λ����)���£�
���� | ��ѧ | Ӣ�� | ��ʷ | ���� | ���� | |
�� | 75 | 93 | 85 | 84 | 95 | 90 |
�� | 85 | 85 | 91 | 85 | 89 | 85 |
���ݱ����е����ݣ��ش��������⣺
(1)���ܷ�Ϊ522�֣����ƽ���ɼ���__________�֣��ҵ��ܷ�Ϊ520�֣�________�ijɼ���һЩ. (������������������)
(2)��������֪![]() . ����Ϊ__________��ƫ�ƣ�(������������������)
. ����Ϊ__________��ƫ�ƣ�(������������������)
(3)����¼ȡʱ����ʷ��������Ŀ��Ȩ����0.3�������Ƴɼ�Ȩ����1������˭�ijɼ�����һЩ����˵������.