题目内容
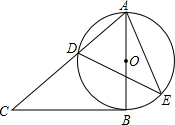
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,点E在中线AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径为( ).

A.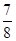 B.
B.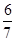 C.
C.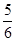 D.1
D.1

A.
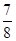 B.
B.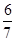 C.
C.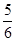 D.1
D.1B.
试题分析:作EH⊥AC于H,EF⊥BC于F,EG⊥AB于G,连结EB,EC,设⊙E的半径为R,如图,
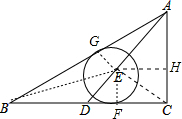
∵∠C=90°,AB=5,AC=3,
∴BC=
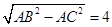 ,而AD为中线,
,而AD为中线,∴DC=2,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EG=EF=R,
∴HC=R,AH=3-R,
∵EH∥BC,
∴△AEH∽△ADC,∴EH:CD=AH:AC,
即EH=
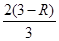 ,
,∵S△ABE+S△BCE+S△ACE=S△ABC,
∴
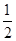 ×5×R+
×5×R+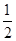 ×4×R+
×4×R+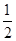 ×3×
×3×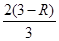 =
=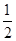 ×3×4,
×3×4,∴R=
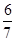 .
.故选B.

练习册系列答案
相关题目
 ,求⊙O的半径.
,求⊙O的半径.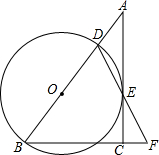
 点
点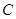 在
在 轴的正半轴上,
轴的正半轴上,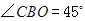 ,
,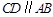 ,
,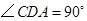 .点
.点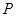 从点
从点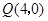 出发,沿
出发,沿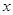 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为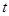 秒.
秒.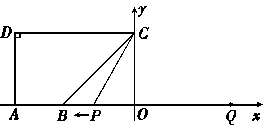
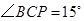 时,求
时,求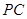 为半径的
为半径的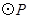 随点
随点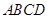 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求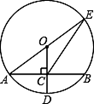
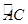 的长.
的长.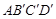 ,则在旋转过程中点D到D’的路径长是
,则在旋转过程中点D到D’的路径长是