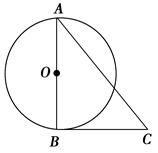
题目内容
如图,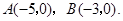 点
点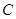 在
在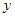 轴的正半轴上,
轴的正半轴上,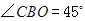 ,
,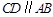 ,
,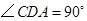 .点
.点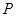 从点
从点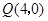 出发,沿
出发,沿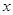 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为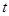 秒.
秒.
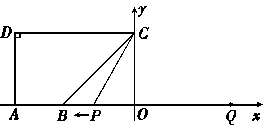
(1)求点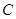 的坐标;
的坐标;
(2)当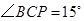 时,求
时,求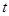 的值;
的值;
(3)以点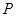 为圆心,
为圆心,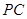 为半径的
为半径的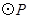 随点
随点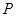 的运动而变化,当
的运动而变化,当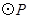 与四边形
与四边形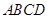 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求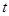 的值.
的值.
 点
点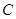 在
在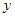 轴的正半轴上,
轴的正半轴上,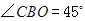 ,
,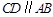 ,
,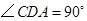 .点
.点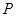 从点
从点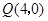 出发,沿
出发,沿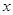 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为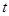 秒.
秒.
(1)求点
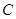 的坐标;
的坐标;(2)当
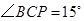 时,求
时,求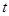 的值;
的值;(3)以点
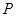 为圆心,
为圆心,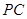 为半径的
为半径的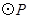 随点
随点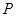 的运动而变化,当
的运动而变化,当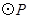 与四边形
与四边形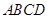 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求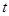 的值.
的值.(1)点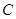 的坐标为(0,3);
的坐标为(0,3);
(2)t的值为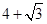 或
或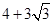 ;
;
(3)t的值为1或4或5.6.
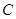 的坐标为(0,3);
的坐标为(0,3);(2)t的值为
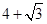 或
或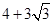 ;
;(3)t的值为1或4或5.6.
试题分析:(1)由∠CBO=45°,∠BOC为直角,得到△BOC为等腰直角三角形,又OB=3,利用等腰直角三角形AOB的性质知OC=OB=3,然后由点C在y轴的正半轴可以确定点C的坐标;
(2)需要对点P的位置进行分类讨论:①当点P在点B右侧时,求出此时的时间t;②当点P在点B左侧时,求出此时的时间t;
(3)当⊙P与四边形ABCD的边(或边所在的直线)相切时,分三种情况考虑:
①当⊙P与BC边相切时,得出此时的时间t;
②当⊙P与CD相切于点C时,P与O重合,可得出P运动的路程为OQ的长,求出此时的时间t;
③当⊙P与CD相切时,得到此时的时间t.
综上,得到所有满足题意的时间t的值.
试题解析:(1)
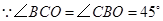 ,
,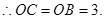
又
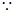 点
点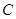 在
在 轴的正半轴上,
轴的正半轴上,  点
点 的坐标为(0,3);
的坐标为(0,3);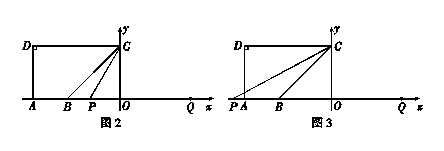
(2)当点
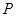 在点
在点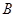 右侧时,如图2.
右侧时,如图2.若
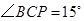 ,得
,得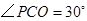 .
.故
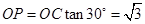 ,此时
,此时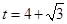 .
.当点
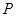 在点
在点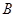 左侧时,如图3,由
左侧时,如图3,由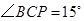 ,
,得
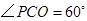 ,故
,故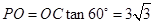 .
.此时
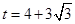 .
.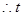 的值为
的值为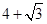 或
或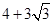 ;
;
(3)由题意知,若
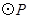 与四边形
与四边形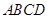 的边相切,有以下三种情况:
的边相切,有以下三种情况:①当
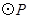 与
与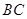 相切于点
相切于点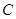 时,有
时,有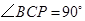 ,从而
,从而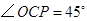 得到
得到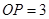 .
.此时
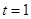 .
. ②当
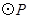 与
与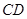 相切于点
相切于点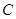 时,有
时,有 ,即点
,即点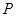 与点
与点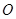 重合,
重合,此时
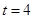 .
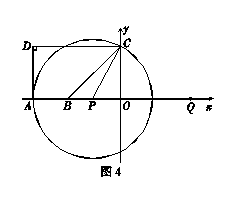
. ③当
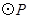 与
与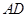 相切时,由题意,
相切时,由题意,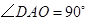 ,
, 点
点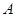 为切点,如图4.
为切点,如图4.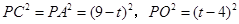 .
.于是
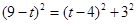 .解出
.解出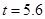 .
.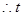 的值为1或4或5.6.
的值为1或4或5.6.
练习册系列答案
相关题目
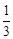 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 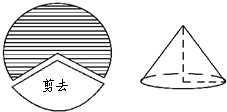
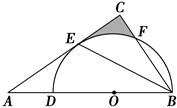
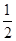 ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.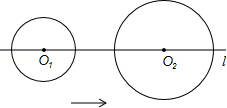
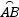 上两点,且∠MEB=∠NFB=60°,则EM+FN= .
上两点,且∠MEB=∠NFB=60°,则EM+FN= .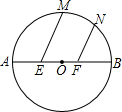
 cm
cm
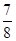 B.
B.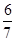 C.
C.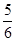 D.1
D.1