题目内容
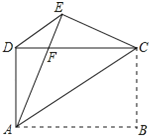
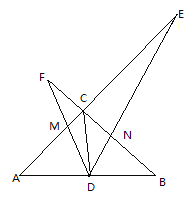
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为E、F,DF与AC交于点M,DE与BC交于点N。
(1)求证:△ADM∽△BND;
(2)在∠EDF绕点D旋转的过程中:
①探究三条线段CD、CE、CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
【答案】(1)(略),(2)①见解析,②![]() .
.
【解析】试题分析:(1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;
(2)①证得△CDF∽△CED,根据相似三角形的性质得到![]() ,即CD2=CECF;
,即CD2=CECF;
②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=![]() ,推出△CEN∽△GDN,根据相似三角形的性质得到
,推出△CEN∽△GDN,根据相似三角形的性质得到![]() =2,根据勾股定理即可得到结论.
=2,根据勾股定理即可得到结论.
(1)证明:∵∠ACB=90°,AC=BC,AD=BD,∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,∴∠DCE=∠DCF=135°,在△DCE与△DCF中,∵CE=CF,∠DCE=∠DCF,CD=CD,∴△DCE≌△DCF,∴DE=DF;
(2)解:①∵∠DCF=∠DCE=135°,∴∠CDF+∠F=180°﹣135°=45°,∵∠CDF+∠CDE=45°,∴∠F=∠CDE,∴△CDF∽△CED,∴ ![]() ,即CD2=CECF;
,即CD2=CECF;
②如图,过D作DG⊥BC于G,则∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,由CD2=CECF得CD=![]() ,∴在Rt△DCG中,CG=DG=CDsin∠DCG=
,∴在Rt△DCG中,CG=DG=CDsin∠DCG=![]() ×sin45°=2,∵∠ECN=∠DGN,∠ENC=∠DNG,∴△CEN∽△GDN,∴
×sin45°=2,∵∠ECN=∠DGN,∠ENC=∠DNG,∴△CEN∽△GDN,∴![]() =2,∴GN=
=2,∴GN=![]() CG=
CG=![]() ,∴DN=
,∴DN=![]() =
=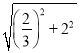 =
=![]() .
.


【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?