题目内容
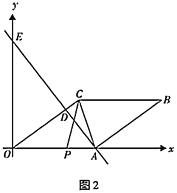
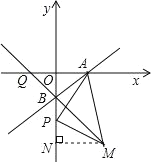
【题目】已知:如图,直线y=x+b与x轴交于点A(2,0),P为y轴上B点下方一点,以AP为腰作等腰直角三角形APM,点M落在第四象限,若PB=m(m>0),用含m的代数式表示点M的坐标是( )

A.(m-2,m+4)B.(m+2,m+4)C.(m+2,-m-4)D.(m-2,-m-4)
【答案】C
【解析】
先利用待定系数法求出直线AB的函数解析式,从而得OP的长,再证△PAO≌△MPN,得到OP=NM,OA=NP,进而用m表示出NM和ON,结合点M在第四象限,表示出点M的坐标即可.
直线y=x+b与x轴交于点A(2,0),
∴0=2+b,解得:b=-2,
∴直线AB的解析式为:y=x2,
令x=0,得y=-2,
∴B(0,-2),
∵PB=m,
∴OP=2+m,
作MN⊥y轴于点N.
∵△APM为等腰直角三角形,PM=PA,
∴∠APM=90°,
∴∠OPA+∠NPM=90°,
∵∠NMP+∠NPM=90°,
∴∠OPA=∠NMP,
在△PAO与△MPN中,
∵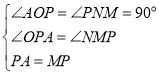 ,
,
∴△PAO≌△MPN(AAS),
∴OP=NM= m+2,OA=NP=2,
∴ON=2+m+2=4+m,MN=OP=2+m,
∵点M在第四象限,
∴点M的坐标为(2+m,4m).
故选C.

练习册系列答案
相关题目