题目内容
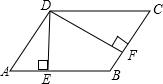
在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,则平行四边形ABCD中∠A的度数是______.
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠DFB=90°,
∵∠EDF+∠DEB+∠B+∠DFB=360°,∠EDF=60°,
∴∠B=120°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠A=60°.
故答案为:60°.
∴∠DEB=∠DFB=90°,
∵∠EDF+∠DEB+∠B+∠DFB=360°,∠EDF=60°,
∴∠B=120°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠A=60°.
故答案为:60°.


练习册系列答案
相关题目